Funkcję kwadratową możemy zapisać, posługując się postacią kanoniczną. Aby lepiej zrozumieć postać kanoniczną, warto przypomnieć sobie najważniejsze informacje o funkcji kwadratowej.
Funkcja kwadratowa – definicja
Funkcja kwadratowa (f) to taka funkcja, w której wzorze:
- musi występować
 ,
, - może występować x,
- może występować liczba stała.
Współczynnik przy czynniku ![]() w funkcji kwadratowej musi być różny od zera. Czynniki b oraz c mogą być dowolne – mogą być również zerami.
w funkcji kwadratowej musi być różny od zera. Czynniki b oraz c mogą być dowolne – mogą być również zerami.
Ogólny wzór funkcji kwadratowej:
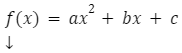
a![]() R\{0}
R\{0}
b,c![]() R
R
a, b i c są współczynnikami funkcji kwadratowej
Postać kanoniczna funkcji kwadratowej
Zapis funkcji kwadratowej w postaci kanonicznej wygląda następująco:
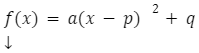
a, p, q – współczynniki liczbowe
a![]() 0
0
Po współczynniku a w funkcji w postaci kanonicznej możemy określić czy ramiona paraboli są skierowane do góry, czy w dół. Jeśli:
- a > 0, to ramiona paraboli są skierowane do góry,
- a < 0, to ramiona paraboli są skierowane w dół.
Dzięki postaci kanonicznej funkcji kwadratowej możemy ułatwić sobie odczytywanie zbioru wartości funkcji i współrzędnych wierzchołka paraboli. p i q są bowiem współrzędnymi wierzchołka.
![]() W – wierzchołek
W – wierzchołek
p,q – współrzędne wierzchołka
Kiedy mamy podaną postać ogólną funkcji, współrzędne wierzchołka możemy obliczyć, korzystając ze wzorów:
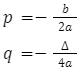
![]()
Oznacza to, że postać kanoniczna wygląda następująco:
![]()
Wzór funkcji w postaci kanonicznej – jak zapisać?
Aby zapisać wzór funkcji w postaci kanonicznej, w pierwszej kolejności odczytaj ze wzoru ogólnego funkcji wartości współczynników. Kiedy posiadasz a, b, c oblicz wyróżnik funkcji korzystając ze wzoru na ![]() .
.
![]()
![]()
Następnie oblicz wartości p i q, podstawiając do wzorów posiadane dane, czyli a, b, c oraz .
Ostatnim etapem jest podstawienie obliczonych wartości do wzoru na postać kanoniczną funkcji:
![]()
Przykład
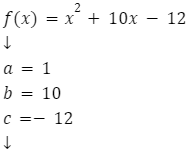
Oblicz wyróżnik funkcji
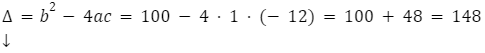
Oblicz wartość p i q.
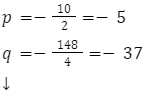
Podstaw obliczone wartości do wzoru na postać kanoniczną.
![]()
Postać kanoniczna nie tylko w matematyce
Z postacią kanoniczną spotykamy się nie tylko w matematyce i w znanej Ci funkcji kwadratowej, którą możemy zamienić właśnie na postać kanoniczną. Ten sposób przedstawiania obiektu jako wyrażenia algebraicznego wykorzystywany jest także w informatyce – w algebrze komputerowej. Postać kanoniczna w algebrze komputerowej oznacza takie przedstawienie, dzięki któremu każdy obiekt ma swoją unikatową reprezentację. Dzięki postaci kanonicznej możemy w prosty sposób sprawdzić równość dwóch obiektów. Zrobimy to właśnie poprzez sprowadzenie ich do postaci kanonicznej. Proces, w którym zamieniamy obiekt na postać kanoniczną, jest określany normalizacją.
