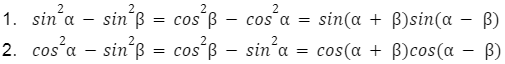Z wzorami redukcyjnymi spotkamy się podczas obliczania wartości funkcji trygonometrycznych. Dzięki nim możliwe jest sprowadzenie wartości funkcji dowolnego kąta do obliczeń wartości dla kąta ostrego, a także kąta o mierze mieszczącej się w zakresie od 90° do 180°.
Wzory redukcyjne
Wzory redukcyjne pozwalają na redukowanie kąta – inaczej argumentu – w funkcjach trygonometrycznych do pierwszej ćwiartki (I ćw.). Funkcje trygonometryczne są okresowe, co oznacza, że wystarczy potrafić zredukować kąty mniejsze od 2 π – 360°.
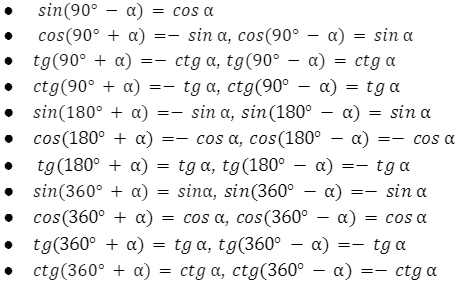
Jak zredukować kąt?
Jak mogłeś zauważyć powyżej, wzorów redukcyjnych jest bardzo wiele, co sprawia, że ich zapamiętanie jest niemożliwe. Warto więc dowiedzieć się, w jaki sposób można je wyznaczyć samodzielnie.
Aby wyprowadzić wzory redukcyjne, wystarczy skorzystać z koła trygonometrycznego.
Aby zredukować kąt w pierwszej kolejności, należy przedstawić kąt pod postacią:
![]() tak, aby kąt był kątem ostrym
tak, aby kąt był kątem ostrym
![]()
![]()
kolejno bierzemy funkcję sinus:
![]()
Pozostałe wzory trygonometryczne
Wzory na tangens i cotangens
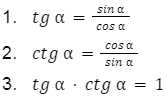
Jedynka trygonometryczna
![]()
Jedynka trygonometryczna jest prawdziwa dla każdej wartości kąta x![]() ℝ
ℝ
Funkcje trygonometryczne podwojonego kąta
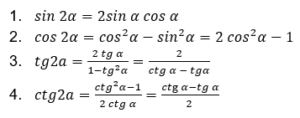
Funkcje trygonometryczne – sumy i różnice kątów
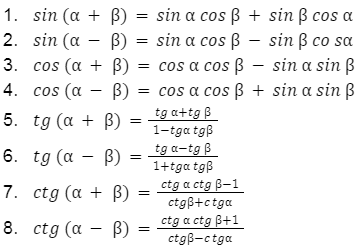
Iloczyn funkcji trygonometrycznych
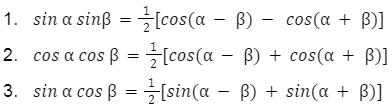
Różnice kwadratów funkcji trygonometrycznych