Całkowanie przez części
Zanim przejdziemy do schematu całkowania przez części, warto powrócić do samej definicji całek. Dzięki temu wszystkie obliczenia będziemy wykonywać szybciej i poprawnie.
Całkowaniem nazywamy działanie odwrotne do różniczkowania. Całka jest oznaczana symbolem:
symbolizuje on łacińskie słowo “Summa”, czyli suma
Zapis całki nieoznaczonej (funkcja pierwotna):
Zapis całki oznaczonej:
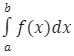
Całką funkcji jest taka funkcja że:
Funkcja , która spełnia ten warunek, jest określana mianem funkcji pierwotnej.
Cała operacja całkowania jest zapisywana:
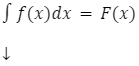
– oznacza, że funkcja f(x) jest poddawana całkowaniu po zmiennej x. Warto pamiętać, że symbol dx należy zawsze zapisywać, nawet jeśli na nic on nie wpływa.
Schemat całkowania
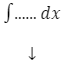w miejscu kropek wpisujemy wzór funkcji, którą całkujemy
Całkowanie przez części
Jeśli funkcje i mają ciągłe pochodne, to:
lub
Przykład
Obliczanie całki
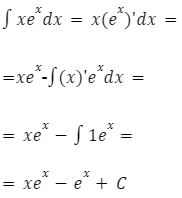
Wzory całkowe wybranych funkcji
Całka funkcji stałej:
Całka funkcji wielomianowej i potęgowej:
Całka funkcji 
:
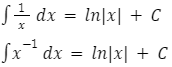
Całka funkcji 
:
Całki funkcji trygonometrycznych:
- sinus
- cosinus
- tangens
- cotangens
Całka funkcji 
:
Całki – zastosowanie
Całki odnajdują zastosowanie w wielu dziedzinach, głównie w fizyce i chemii. Dzięki całkom możemy m.in. obliczyć objętości kształtów nieregularnych, które nie jesteśmy w stanie obliczyć z podstawowych, dobrze nam znanych wzorów. Co ciekawe całka może określać różne pojęcia – są one jednak ze sobą mocno powiązane. Najczęściej całka oznacza jednak całkę oznaczoną bądź całkę nieoznaczoną. Jeśli masz trudności z przybliżeniem sobie definicji całki, wyobraź sobie sumę nieskończenie wielu nieskończenie małych wartości. Możemy je np. otrzymać przez pomnożenie funkcji przez nieskończenie małą różniczkę jej zmiennej. Oprócz całki oznaczonej i nieoznaczonej możemy spotkać – choć znacznie rzadziej – inne rodzaje całek, takie jak: całki krzywoliniowe, całki powierzchniowe, całki podwójne, całki eliptyczne, całki wymiany czy całki J. Jak sam widzisz, całki są nieodłącznym elementem wielu dziedzin naukowych.
