Zanim zapoznasz się z całkowaniem przed podstawianie, warto powrócić do samej definicji całek. Dzięki temu wszystkie obliczenia będziesz wykonywać szybciej i poprawnie.

 

Całkowaniem nazywamy działanie odwrotne do różniczkowania. Całka jest oznaczana symbolem:

całkowanie przez podstawianie 1symbolizuje on łacińskie słowo “Summa”, czyli suma

 

Zapis całki nieoznaczonej (funkcja pierwotna):

całkowanie przez podstawianie 2

Zapis całki oznaczonej:

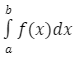
całkowanie przez podstawianie 3

 

Całką funkcji całkowanie przez podstawianie 4 jest taka funkcja całkowanie przez podstawianie 5 że:

całkowanie przez podstawianie 6
Funkcja całkowanie przez podstawianie 5 która spełnia ten warunek, jest określana mianem funkcji pierwotnej.

 

Cała operacja całkowania jest zapisywana:

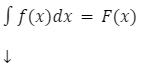
całkowanie przez podstawianie 7
całkowanie przez podstawianie 8 – oznacza, że funkcja f(x) jest poddawana całkowaniu po zmiennej x. Pamiętaj, że symbol dx należy zawsze zapisywać, nawet jeśli na nic on nie wpływa.

 

Schemat całkowania 

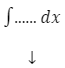całkowanie przez podstawianie 9w miejscu kropek powinien znaleźć się wzór funkcji, którą całkujemy

Całkowanie przez podstawianie

Tego rodzaju całkowanie wykorzystujemy, kiedy wśród funkcji podcałkowej jesteśmy w stanie wyodrębnić pewną funkcję oraz jej pochodną.

Funkcja całkowanie przez podstawianie 4 może zostać zapisana w następujący sposób:

całkowanie przez podstawianie 10
strzałka
funkcja całkowanie przez podstawianie 11 posiada pochodną:

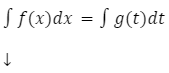
całkowanie przez podstawianie 12

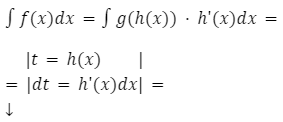
całkowanie przez podstawianie 13
w pierwszej linii oznaczamy, za co podstawiamy, w drugiej z kolei obliczamy pochodne, tego co znajduje się wyżej – osobno dla lewej oraz osobno dla prawej strony.

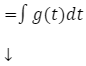
całkowanie przez podstawianie 14
Po prawej stronie zmienna to “x’ więc po obliczeniu pochodnej należy dopisać “dx”. Analogicznie, gdy po lewej stronie zmienną jest “t” to po obliczeniu pochodnej należy dopisać “dt”.

Całkowanie przez części

Jeśli funkcje f i h mają ciągłe pochodne, to:

całkowanie przez podstawianie 15

lub

całkowanie przez podstawianie 16

 

Przykład

Obliczanie całki całkowanie przez podstawianie 17

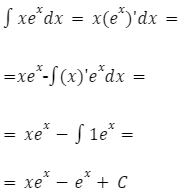
całkowanie przez podstawianie 18

Całki w nauce

Całki odnajdują zastosowanie w wielu dziedzinach naukowych – najczęściej w fizyce i chemii. Dzięki nim możemy m.in. obliczyć objętości kształtów nieregularnych, które nie jesteśmy w stanie obliczyć z podstawowych, dobrze nam znanych wzorów. Co ciekawe całka może określać różne pojęcia – są one jednak ze sobą mocno powiązane. Najczęściej oznacza jednak całkę oznaczoną lub całkę nieoznaczoną. Jeśli masz trudności z przybliżeniem sobie definicji całki, wyobraź sobie sumę nieskończenie wielu nieskończenie małych wartości. Możemy je np. otrzymać przez pomnożenie funkcji przez nieskończenie małą różniczkę jej zmiennej. Oprócz całki oznaczonej i nieoznaczonej możemy spotkać: całki krzywoliniowe, całki powierzchniowe, całki podwójne, całki eliptyczne, całki wymiany.