Cięciwa okręgu to odcinek, który łączy dowolne dwa punkty leżące na tym okręgu. Jeden okrąg może mieć nieskończenie wiele cięciw. Co ważne, mogą mieć one – jednak nie muszą – taką samą długość. Pojęcie cięciwy nie dotyczy wyłącznie okręgu, ale również koła.

 

Szczególnym rodzajem cięciwy jest średnica. Jest to również odcinek łączący dwa dowolne punkty okręgu, jednak przechodzi także przez sam środek okręgu.

 

Ważne: Środek nie należy do okręgu. Okrąg to bowiem zbiór wyłącznie tych punktów położonych na brzegu koła. Przy pojęciu cięciwy warto wspomnieć o różnicach między kołem i okręgiem.

 

Koło jest zbiorem punktów na płaszczyźnie, których odległość od środka jest mniejsza bądź równa promieniowi koła.

 

Okrąg możemy w najprostszy sposób nazwać brzegiem koła.

Cięciwa okręgu – zależności

Dla cięciw okręgu zachodzą następujące zależności:

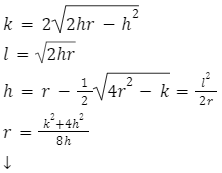
k – długość cięciwy, która łączy punkty A i B
l – długość cięciwy, która łączy punkty B i C
h – wysokość łuku okręgu
r – promień okręgu

 

Wszystkie dane zostały przeniesione na poniższy rysunek:

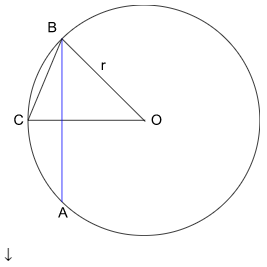
O – środek okręgu
AB – cięciwa

Okrąg i koło – pozostałe definicje

Cięciwa nie jest jedynym pojęciem charakterystycznym dla koła i okręgu. Oprócz niej możemy wyróżnić również: średnicę i styczną.

Średnica to cięciwa, która przechodzi przez środek okręgu.

Styczna to prosta, która ma z okręgiem wyłącznie jeden punkt wspólny.

 

Pole koła 

Pole koła obliczamy ze wzoru:

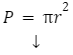r – promień koła

 

Do obliczenia pola koła używamy stałej pi: 3,14. Po dokonanym obliczeniu wynik otrzymujemy w jednostkach kwadratowych. Zwykle wynik pozostawiamy w formie, w której występuje π, jako że pi jest wartością stałą. Możemy jednak podstawić pod nią 3,14, by otrzymać wynik z dokładnością do dwóch miejsc po przecinku.

 

Obwód koła 

Obwód koła jest niczym innym jak długością okręgu. Z definicji okręgu możemy bowiem dowiedzieć się, że jest to brzeg koła. Aby obliczyć obwód, wystarczy skorzystać z następującego wzoru:

r – promień koła

 

Obliczanie pola i obwodu koła bez długości promienia 

Może się zdarzyć, że będziemy musieli obliczyć pole bądź obwód koła bez znajomości długości jego promienia. W takich sytuacjach otrzymujemy jednak zazwyczaj inne wartości – najczęściej długość średnicy. Korzystając z definicji średnicy, dokonanie obliczeń będzie bardzo proste. Wystarczy wówczas wiedzieć, że średnicę tworzą dwa promienie. Aby uzyskać długość promienia, wystarczy więc podzielić długość średnicy przez 2. Otrzymany wynik podstawiamy do wzoru na pole lub obwód koła.