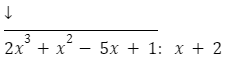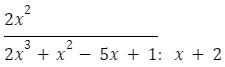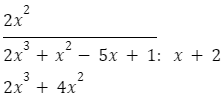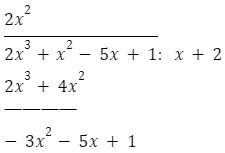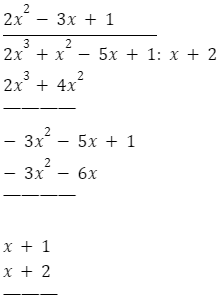Dzielenie wielomianów może odbywać się z wykorzystaniem tradycyjnej metody lub przy użyciu schematu Hornera. Aby w pełni zrozumieć sposób dzielenia wielomianów, warto powrócić do samej definicji tego działania.
Podzielność wielomianów – najważniejsze definicje
Wielomian P(x) będzie podzielny przez wielomian Q(x) wyłącznie, gdy istnieje taki wielomian S(x), który spełnia równanie:
![]()
Ważne: Przy dzieleniu wielomianu przez inny wielomian istnieje możliwość otrzymania reszty z dzielenia. Reszta z dzielenia wielomianu W(x) przez dwumian x to W(a).
W(x) oraz P(x) są wielomianami, a dodatkowo P(x) nie jest wielomianem zerowym. W takim przypadku istnieją dwa takie wielomiany Q(x) i R(x) spełniające równanie:
![]()
w którym stopień wielomianu R(x) jest mniejszy od stopnia wielomianu P(x).
Wielomianem jest funkcja jednej zmiennej w potędze 3 bądź wyższej. Wielomian jednej zmiennej x ![]() ℝ to funkcja określona wzorem:
ℝ to funkcja określona wzorem:
![]()
![]()
n ![]() ℕ- stopień wielomianu
ℕ- stopień wielomianu
![]()
![]() ℝ- współczynniki wielomianu
ℝ- współczynniki wielomianu
![]() – wyraz wolny wielomianu
– wyraz wolny wielomianu
![]()
![]() 0-wyraz przy najwyższej potędze
0-wyraz przy najwyższej potędze
Stopniem wielomianu nazywamy najwyższy wykładnik potęgi zmiennej wielomianu dla niezerowego współczynnika.
Jednomian a wielomiany
Jednomianem określamy wyrażenie algebraiczne, które składa się z jednej liczby i ewentualnie jednej lub kilku liter. Kolejno możemy wyróżnić dwumian, składający się z dwóch jednomianów, które są połączonych ze sobą znakiem dodawania, bądź odejmowania. Kolejno możemy wyliczać trójmiany itd., jednak dużo prościej jest używać określenia wielomiany. Już sam dwumian jest wielomianem.
Dzielenie wielomianów
- Pierwszym krokiem podczas dzielenia wielomianów jest zapisanie wielomianów pod inną postacią:
-
- wielomian
 przez dwumian
przez dwumian 

- wielomian
- Następnie pierwsze składniki wielomianu dzielimy przez pierwszy składnik dwumianu.pierwszy składnik wielomianu:

pierwszy składnik dwumianu: x

- Wynik powyższego dzielenia:
 mnożymy przez dwumian. Wynik należy zapisać pod wielomianem.
mnożymy przez dwumian. Wynik należy zapisać pod wielomianem.

- W następnej kolejności należy wykonać odejmowanie: od wielomianu odejmujemy wielomian, który jest zapisany pod nim. Otrzymany wynik należy zapisać pod kreską.

- Kolejne operacje wykonujemy tak samo jak poprzednie. W momencie, gdy uzyskamy wielomian o stopniu niższym, od tego, przez który dzielimy, algorytm się kończy.

-1
- Resztą z dzielenia wielomianu jest otrzymana liczba -1. Wielomian ten możemy zapisać pod postacią: