Funkcję wykładniczą zapisujemy wzorem:

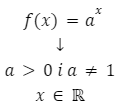
powyższy wzór możemy także zapisać używając symbolu y:

 

Sama nazwa funkcji wykładniczej pochodzi od x znajdującego się w wykładniku. To, jaki kształt przyjmie wykres, uzależnione jest od tego, czy a > 1, czy a < 1.

Tylko dla a > 0 jesteśmy w stanie jednoznacznie określić funkcję dla każdej liczby rzeczywistej x. Kiedy a < 0 funkcja nie mogłaby być określona dla każdej liczby rzeczywistej (na przykład w przypadku a =-5 i nie jesteśmy w stanie dokonać obliczeń, ponieważ musielibyśmy obliczyć pierwiastek kwadratowy z liczby ujemnej – który nie istnieje).

 

Kiedy a=0 nie możemy określić funkcji dla żadnej liczby x niedodatniej, gdyż wiązałoby się to z dzieleniem przez 0, a wiadomo, że dzielić przez zero nie można.

 

Wykres funkcji

 

Funkcja przyjmuje postać krzywej, zawsze przecinającej się na osi OY w punkcje 1.

Rysowanie wykresu funkcji wykładniczej

Przed naniesieniem funkcji wykładniczej na układ współrzędnych należy ustalić, czy a > 1 czy a < 1.

Kiedy:

• a > 1, to funkcja wykładnicza jest ściśle rosnąca,
• a < 1, to funkcja wykładnicza jest ściśle malejąca.

Kolejnym krokiem do narysowania funkcji wykładniczej na układzie współrzędnych będzie wyznaczenie dowolnych punktów. Warto w tym celu narysować tabelę.

 

Przykład

Dana jest funkcja:

Z powyższej funkcji wynika, że a jest liczbą dodatnią, a więc funkcja ta będzie rosnąca. Kolejnym krokiem będzie narysowanie tabeli, która ułatwi wyznaczenie punktów należących do wykresu tej funkcji wykładniczej. Poniżej możesz zapoznać się z przykładową tabelą. W miejsce x możesz podstawić dowolną liczbę.

 

x	-2	0	1	2
		1	2	4

 

Mając przykładowe współrzędne funkcji wykładniczej, możesz nanieść je na układ współrzędnych i połączyć. Im więcej dowolnych punktów wyznaczysz, tym dokładniejszy wykres funkcji uzyskasz. Pamiętaj, aby łącząc punkty przeciąć oś OY w punkcie 1.

Podstawa a > 1 – własności funkcji

Kiedy a > 1, to możemy wyróżnić następujące własności funkcji wykładniczej:

• dziedziną funkcji wykładniczej są wszystkie liczby rzeczywiste: ℝ,
• zbiorem wartości funkcji wykładniczej są wyłącznie liczby rzeczywiste dodatnie: ,
• monotoniczność – funkcja wykładnicza jest rosnąca,
• różnowartościowość – funkcja wykładnicza jest różnowartościowa,
• funkcja wykładnicza nie ma miejsc zerowych.

 

Kiedy a < 1, to możemy wyróżnić następujące własności funkcji wykładniczej:

• dziedziną funkcji wykładniczej są liczby rzeczywiste:  ℝ,
• zbiorem wartości funkcji wykładniczej są wyłącznie liczby rzeczywiste dodatnie: ,
• monotoniczność – funkcja wykładnicza jest malejąca,
• różnowartościowość – funkcja wykładnicza jest różnowartościowa,
• funkcja wykładnicza nie ma miejsc zerowych.