Definicje funkcji trygonometrycznych
Kiedy jeden z kątów trójkąta posiada 90°, jeden z jego kątów ostrych możemy oznaczyć literą .
Gdy literą a i b oznaczymy dodatkowo przyprostokątne trójkąta prostokątnego, z kolei przeciwprostokątną literą c, możemy wyszczególnić poniższe definicje funkcji trygonometrycznych:

Sinus kąta ostrego
Do obliczenia sinusa kąta ostrego w trójkącie prostokątnym potrzebujesz boku leżącego naprzeciw tego kąta oraz przeciwprostokątną.
Cosinus kąta ostrego
Do obliczenia cosinusa kąta ostrego w trójkącie prostokątnym będziesz potrzebować przyprostokątną, która leży przy tym kącie oraz przeciwprostokątną.
Tangens kąta ostrego
Aby obliczyć tangens kąta ostrego w trójkącie posiadającym kąt prosty, potrzebujesz bok leżący naprzeciwko tego kąta (będzie to jedna z przyprostokątnych) i drugą przyprostokątną.
Cotangens kąta ostrego
Do obliczenia cotangensa w trójkącie prostokątnym potrzebujesz przyprostokątną leżącą przy tym kącie oraz drugą przyprostokątną.
Tabela funkcji trygonometrycznych dla niektórych miar kąta
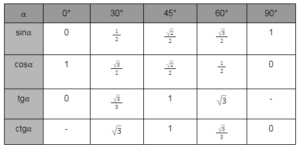
Aby odczytać wartości funkcji dla danych miar kąta, można posłużyć się tablicą wartości funkcji trygonometrycznych. Tablice te są ogólnodostępne i mogą z nich korzystać nawet maturzyści. Znajdują się one na końcu tablic matematycznych CKE. Poniżej możesz zapoznać się z tabelą wartości funkcji trygonometrycznych dla najczęściej spotykanych kątów.
Funkcje trygonometryczne w trójkącie prostokątnym w codziennym życiu
Trygonometria pozwala nam na dokonywanie wielu obliczeń dotyczących wielkości, niemal niemożliwych do zmierzenia w inny, bardziej bezpośredni sposób. To właśnie ona pozwala nam na obliczenie długości podjazdów dla osób niepełnosprawnych czy prawidłowego nachylenia drogi, która ma zostać wybudowana na zboczu.
Funkcje trygonometryczne są więc niezbędne do precyzyjnego sporządzania map z uwzględnieniem wysokości między wybranymi punktami w terenie. Co ciekawe trygonometria znalazła swoje zastosowanie nawet w branży informatycznej – stanowi niezwykle ważny element szeregów Fouriera używanych podczas kompresji danych. Nic więc dziwnego, że w trakcie nauki szkolnej tak wiele uwagi jest poświęcanej właśnie trygonometrii.
