Graniastosłup prawidłowy czworokątny jest specyficznym rodzajem graniastosłupa, który w swojej podstawie posiada kwadrat. Wszystkie ściany graniastosłupa prawidłowego czworokątnego są prostokątami prostopadłymi do podstawy.

 

Graniastosłup prawidłowy czworokątny ma:

• 12 krawędzi,
• 8 wierzchołków,
• 6 ścian.

 

Gdy w graniastosłupie prawidłowym czworokątnym wysokość będzie miała taką samą długość, jak ściana boczna, to otrzymamy sześcian.

Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego

Do obliczenia pola powierzchni całkowitej tej figury będziemy potrzebować długości boku podstawy i wysokości graniastosłupa. Wzór na pole całkowite wygląda następująco:

Pp – pole podstawy
Pb – pole boczne

 

Jako że w podstawie graniastosłupa prawidłowego czworokątnego znajduje się kwadrat, do obliczenia jej pola będzie nam potrzebna wyłącznie jedna długość:

Do obliczenia pola powierzchni bocznej graniastosłupa potrzebna będzie wysokość. W przypadku tej figury ścianą boczną jest prostokąt (może także być kwadrat). Pamiętajmy o tym, aby otrzymany wynik przy obliczaniu pola jednej ściany pomnożyć przez ilość ścian, czyli 4.

Ostatecznie wzór na pole całkowite graniastosłupa prawidłowego czworokątnego możemy zapisać:

Objętość graniastosłupa prawidłowego czworokątnego

Do obliczania objętości graniastosłupa prawidłowego czworokątnego nie potrzebujemy zbyt wielu danych. Wystarczy tylko pole podstawy i wysokość. Wzór wygląda następująco:

Przekątna graniastosłupa prawidłowego czworokątnego

W każdym graniastosłupie prawidłowym czworokątnym możemy poprowadzić odcinek, który łączy dwa najdalsze jego wierzchołki. Odcinek ten nosi nazwę przekątnej. Aby obliczyć długość przekątnej, musimy posiłkować się twierdzeniem Pitagorasa. Zgodnie z nim wzór wygląda następująco:

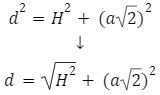
Graniastosłupy – inne rodzaje

Graniastosłup prawidłowy czworokątny nie jest jedynym specyficznym rodzajem graniastosłupa. Oprócz niego możemy także spotkać się z:

• graniastosłupem prawidłowym trójkątnym,
• graniastosłupem prawidłowym sześciokątnym

 

W graniastosłupie prawidłowym trójkątnym mamy do czynienia z charakterystyczną podstawą, jaką jest trójkąt równoboczny. Posiada on 5 ścian, 6 wierzchołków i 9 krawędzi.

 

Jak łatwo się domyślić podstawę graniastosłupa prawidłowego sześciokątnego stanowi sześciokąt foremny. Wszystkie ściany tego graniastosłupa są prostokątami prostopadłymi do podstawy. Graniastosłup prawidłowy sześciokątny ma 8 ścian, 12 wierzchołków i 18 krawędzi.