Hiperbolę tworzy krzywa, która jest zbiorem punktów, dla których wartość bezwzględna różnicy odległości tych właśnie punktów od dwóch innych ustalonych punktów jest stała. Wspomniane dwa ustalone punkty są określane ogniskami hiperboli.

 

Hiperbola jest wykresem funkcji , w której skład wchodzą niejako dwie części. Pierwsza z nich jest przedziałem od minus nieskończoności do 0, druga z kolei dotyczy przedziału od zera do plus nieskończoności. Oba przedziały są przedziałami otwartymi.

 

Wykres można zapisać przez oraz

 

Z ciekawostek warto wiedzieć, że nazwę hiperboli wprowadził grecki matematyk Apoloniusz z Pergi. Sposób wykorzystania paraboli został jednak dostrzeżony znacznie później, bo dopiero w XVII w.

Asymptota hiperboli – definicja

Asymptotą hiperboli jest prosta, do której wykres się zbliża, jednak nigdy jej nie dotyka. Dla hiperboli a/x asymptotami są osie układu współrzędnych, czyli oś X jest asymptotą poziomą dla hiperboli, z kolei oś Y stanowi asymptotę pionową dla hiperboli.

Rysowanie hiperboli

Aby nanieść hiperbolę na układ współrzędnych konieczne będzie wyznaczenie kilku punktów i .

 

Kolejnym krokiem jest narysowanie hiperboli, której asymptotami są osie układu współrzędnych. Możemy wyznaczać dowolną ilość punktów należących do wykresu hiperboli. Musimy wiedzieć, że im więcej ich wyznaczymy przed narysowaniem, tym dokładniejszy wykres hiperboli otrzymamy.

 

Przykład

wyznaczanie punktów należących do wykresu funkcji:

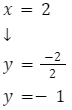
Do funkcji należy punkt o współrzędnych A=(2,1)

Dla x>0

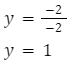
Do funkcji należy punkt o współrzędnych B=(-2,1)

 

Po podstawieniu za x dowolnych liczb otrzymamy kilka punktów o dokładnych współrzędnych, które wystarczy nanieść na układ współrzędnych. Warto zwiększać ilość wyliczonych punktów, aby uzyskać jak najdokładniejszy wykres.

 

Przykład 2

Gdy do wzoru funkcji  dodamy 1, a więc otrzymamy , to każdy punkt z wykresu, który został narysowany, przesunąłby się o jedną jednostkę do góry. To oznacza, że nasza asymptota pozioma uległaby zmianie. Analogicznie odejmując jakąś liczbę, asymptota idzie w dół.

Średnica hiperboli

Średnica hiperboli to odcinek przechodzący przez środek hiperboli. Końce tego odcinka leżą na hiperboli.

 

Hiperbola a parabola

Często spotykanym błędem jest mylenie hiperboli z parabolą. Choć pojęcia te są do siebie podobne, podobieństwo to wynika tylko z nazwy.

Parabolą nazywamy wykres każdej funkcji kwadratowej. Parabola składa się z wierzchołka i ramion paraboli, które mogą być skierowane w dół lub w górę w zależności od wartości współczynnika  we wzorze funkcji kwadratowej.

Jeśli:

•  to ramiona paraboli skierowane są do góry,
•  to ramiona paraboli skierowane są w dół.

Wierzchołek paraboli (W) możemy obliczyć, korzystając z ogólnego wzoru funkcji kwadratowej.