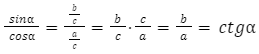Jedynką trygonometryczną określamy tożsamość geometryczną, która przyjmuje postać:
![]()
Jedynka trygonometryczna – dowód dla kąta ostrego w trójkącie prostokątnym
Definicje funkcji trygonometrycznych mówią nam, że:
![]()
![]()
![]()
![]()
Twierdzenie Pitagorasa mówi nam, że:
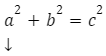
w poniższym wzorze podstawiamy ![]() za
za ![]()
![]()
Tangens i cotangens – wzory
Dla wybranego, dowolnego kąta zachodzą wzory:




Dla wybranego kąta ostrego funkcje trygonometryczne muszą być określone, aby zaszły powyższe wzory.Wzory te są prawdziwe dla każdego kąta ostrego, a także dla wszystkich kątów, dla których funkcje są określone – czyli kiedy nie pojawia się w mianowniku dzielenie przez zero.
Wzory dla kąta ostrego w trójkącie prostokątnym
Znając wartość minimum jednej funkcji trygonometrycznej, możemy obliczyć wartości wszystkich pozostałych funkcji. Możemy to zrobić, korzystając z poniższych wzorów.
Przykład
Dany jest sinus ![]() . Ile wynosi
. Ile wynosi ![]() oraz
oraz ![]() ?
?
Zgodnie z jedynką trygonometryczną:
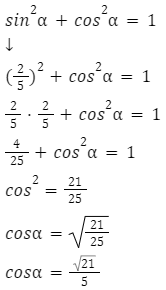
Kolejnym krokiem jest obliczenie ![]() , należy więc skorzystać z wzoru na tangensa:
, należy więc skorzystać z wzoru na tangensa:
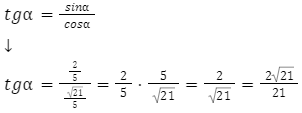
W następnej kolejności obliczamy ![]() . Tu również korzystamy z wzoru na cotangens:
. Tu również korzystamy z wzoru na cotangens:
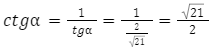
Z powyższych obliczeń otrzymujemy:
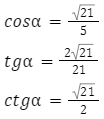
Sinus, cosinus, tangens, cotangens – definicje
Poznałeś wzór na jedynkę trygonometryczną, a także na tangens i cotangens. Aby w pełni zrozumieć schematy obliczeń, warto powrócić do podstawowych definicji, by je utrwalić.
Sinusem kąta nazywamy stosunek długości przyprostokątnej, która leży naprzeciw kąta do długości przeciwprostokątnej.
Cosinusem kąta określamy stosunek długości przyprostokątnej, która leży przy kacie do długości przeciwprostokątnej.
Tangensem kąta określamy stosunek długości przyprostokątnej, która leży naprzeciw kąta do długości drugiej przyprostokątnej, która z kolei leży przy tym kącie.
Cotangensem kąta nazywamy stosunek długości przyprostokątnej, która leży przy kącie do długości drugiej przyprostokątnej, leżącej naprzeciw tego kąta.
Wszystkie powyższe stosunki są określane funkcjami trygonometrycznymi kąta .
Ważne: Wszystkie stosunki nie zależą od wielkości trójkąta, a wyłącznie od kąta .