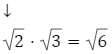Liczby niewymierne to wszystkie te liczby, których nie możemy zapisać za pomocą ułamka zwykłego. Wraz z liczbami wymiernymi, liczby niewymierne tworzą zbiór liczb rzeczywistych.

 

Liczby niewymierne – przykłady

Do liczb niewymiernych możemy zaliczyć m.in.: liczby niewymierne 1

Warto jednak zaznaczyć, że nie każdy pierwiastek jest liczbą niewymierną. Niektóre z nich możemy zapisać za pomocą ułamka zwykłego. Przykładem tego jest, chociażby: liczby niewymierne 2

liczby niewymierne 3

Liczby niewymierne, a liczby wymierne

Między dwiema różnymi liczbami rzeczywistymi znajdziemy liczby niewymierne. Przykładem takiej liczby jest pierwiastki 13. Skąd wiemy, że liczba ta jest niewymierna?

Aby udowodnić, że liczba pierwiastki 13 jest niewymierna, warto na chwile założyć, że jest zupełnie odwrotnie. Jeśli tak by było, to znaczyłoby, że:

liczby niewymierne 4 m,n – liczby całkowite, n różne od 0
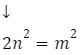
liczby niewymierne 6

Ostatnia z równości nie może być prawdziwa, ponieważ oznaczałaby, że przy rozkładzie na czynniki pierwsze liczba 2 występuje parzystą liczbę razy po prawej stronie i nieparzystą po lewej. W takiej sytuacji otrzymujemy sprzeczność.

 

Powyższy dowód niewymierności pierwiastki 13 jest dowodem przez sprowadzenie do sprzeczności. Dowód na sprowadzenie do sprzeczności polega na udowodnieniu, że przyjęcie prawdziwości jakiegoś zdania prowadzi do sprzeczności.

 

Suma liczby wymiernej i niewymiernej

Warto wiedzieć, że zawsze suma liczby wymiernej i niewymiernej będzie liczbą niewymierną:

  • liczby niewymierne 7 daje liczbę niewymierną
  • liczby niewymierne 8 daje liczbę niewymierną

 

Iloczyn dwóch liczb niewymiernych

Iloczyn dwóch liczb, które są niewymierne, może być liczbą wymierną lub niewymierną:

  • liczby niewymierne 9 daje liczbę wymierną
    liczby niewymierne 10
  • liczby niewymierne 11 daje liczbę niewymierną
    liczby niewymierne 12

Liczby wymierne – definicja

Wiesz już, że liczby niewymierne wraz z liczbami wymiernymi tworzą zbiór liczb rzeczywistych. Czym w takim razie są liczby wymierne?

 

Liczbami wymiernymi nazywamy liczby, które możemy zapisać w postaci ilorazu dwóch liczb całkowitych, gdzie dzielnik jest różny od 0. Upraszczając – są to liczby, które możemy przedstawić, wykorzystując ułamek zwykły.

 

Zbiór liczb wymiernych oznaczany jest symbolem ℚ

Postać ułamka zwykłego możemy z kolei zapisać następująco:

liczby niewymierne 13p – dowolna liczba całkowita
q – dowolna liczba całkowita różna od 0

 

Zbiór liczb wymiernych możemy zapisać, wykorzystując następujący zapis:

liczby niewymierne 14

 

Każda liczba całkowita jest liczbą wymierną. Dodatkowo każdą liczbę możemy zapisać za pomocą ułamka, wykorzystując przy tym różne sposoby.