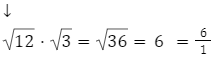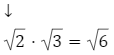Liczbami wymiernymi nazywamy liczby, które możemy zapisać w postaci ilorazu dwóch liczb całkowitych, gdzie dzielnik jest różny od 0. Upraszczając – są to liczby, które możemy przedstawić za pomocą ułamka zwykłego.

 

Zbiór liczb wymiernych oznaczany jest symbolem liczby wymierne 1

Postać ułamka zwykłego możemy z kolei zapisać następująco:

liczby wymierne 2p – dowolna liczba całkowita
q – dowolna liczba całkowita różna od 0

 

Zbiór liczb wymiernych możemy zapisać, wykorzystując następujący zapis:

liczby wymierne 3

 

Ważne

Każda liczba całkowita jest liczbą wymierną. Dodatkowo każdą liczbę możemy zapisać za pomocą ułamka, wykorzystując przy tym różne sposoby.

 

Dla przykładu liczbę całkowitą 1 możemy zapisać w postaci ułamka zwykłego:

liczby wymierne 4

Przykład 2

liczby wymierne 5

Przykład 3

liczby wymierne 6

 

Ułamki dziesiętne także są liczbami wymiernymi

Przykłady

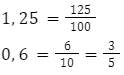
liczby wymierne 7

liczby wymierne 8jak widzisz, ułamek okresowy także jest liczbą wymierną

 

Jakie liczby nie będą liczbami wymiernymi?

Liczby, które nie możemy zapisać w postaci ułamka zwykłego to liczby niewymierne. Przykładem jednej z nich jest pierwiastek z trzech. Liczby wymierne wraz z liczbami niewymiernymi składają się na zbiór liczb rzeczywistych.

 

Przykłady liczb niewymiernych:

liczby wymierne 9

 

Ważne:

Warto pamiętać, że nie każdy pierwiastek będzie liczbą niewymierną. Przykładem tego jest chociażby

liczby wymierne 10

Suma liczby wymiernej i niewymiernej

Warto wiedzieć, że zawsze suma liczby wymiernej i niewymiernej będzie liczbą niewymierną:

  • liczby wymierne 11 daje liczbę niewymierną
  • liczby wymierne 12 daje liczbę niewymierną

 

Iloczyn dwóch liczb niewymiernych

Iloczyn dwóch liczb, które są niewymierne, może być liczbą wymierną lub niewymierną:

  • liczby wymierne 13 daje liczbę wymierną
    liczby wymierne 14
  • liczby wymierne 16 daje liczbę niewymierną
    liczby wymierne 17

 

Liczby wymierne a liczby całkowite

Liczby całkowite należą do zbioru liczb wymiernych. Liczby całkowite z kolei to liczby naturalne dodatnie i liczby do nich przeciwne. Zbiór liczb całkowitych oznaczany jest literą C. W przypadku liczb wymiernych, czyli liczb, które możemy zapisać jako iloraz , staramy się najczęściej o zapis w postaci nieskracalnej.

 

Przykład

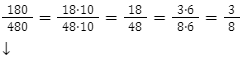
liczby wymierne 18
otrzymany ułamek liczby wymierne 19 jest ułamkiem nieskracalnym. Kiedy doprowadzimy ułamek do postaci nieskracalnej, licznik i mianownik stają się liczbami względnie pierwszymi. Oznacza to, że nie mają żadnych wspólnych dzielników całkowitych oprócz 1 i -1.