Mediana – definicja

Mediana jest wartością, która dzieli zbiór danych na dwie części, tak że powyżej i poniżej niej znajduje się taka sama wartość danych. Inaczej mówiąc, medianę możemy określić mianem wartości środkowej.

Wyznaczanie mediany

Mediana może być:

• wartością środkową,
• średnią arytmetyczną dwóch środkowych elementów.

 

Wartość środkowa

Mediana jest wartością środkową jeśli w posortowanym zbiorze jest nieparzysta liczba danych.

 

Średnia arytmetyczna

Jeśli zbiór posortowanych danych jest liczbą parzystą, to mediana jest średnią arytmetyczną dwóch środkowych elementów tego zbioru.

 

Przykład 1

Podany jest zbiór liczb {5,9,34,2,78,10}

Pierwszym krokiem do obliczenia mediany będzie posortowanie powyższego zbioru

 

{2,5,9,10,34,78}

Powyższy zbiór składa się z 6 elementów:
 n jest parzysta, co oznacza, że do obliczenia mediany konieczne będzie znalezienie dwóch środkowych elementów zbioru i obliczenie ich średniej arytmetycznej. W przypadku tak niewielkiego zbioru nie będzie to trudne zadanie, ponieważ wszystkie elementy są widoczne. Dwa środkowe elementy to 9 i 10. Kiedy jednak zbiór jest rozbudowany, konieczne będzie wykorzystanie podanego wyżej wzoru.

 

Obliczenie mediany w tym przypadku wygląda następująco:

 

Przykład 2

Podany jest zbiór liczb: {6,15,5,90,43,145,7}

Po posortowaniu wygląda on następująco:

{5,6,7,15,43,90,145}

Powyższy zbiór składa się z 7 elementów:   n to liczba nieparzysta, co oznacza, że medianą jest liczba środkowa – w tym przypadku 4ty element, czyli liczba 15. Przy większym zbiorze konieczne będzie jednak skorzystanie ze wzoru na medianę zbioru o nieparzystej liczbie elementów:

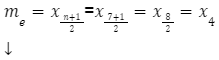
z obliczeń wynika, że medianą jest czwarty element zbioru, czyli w tym przypadku jest to 15.

Mediana – zastosowanie w życiu codziennym

Obecność mediany jest nieoceniona w dokonywaniu wszelkiego rodzaju statystyk. To właśnie dzięki niej możliwe jest podzielenie badanych na 2 grupy o takiej samej liczbie osób. Grupa badawcza może być rozdzielona ze względu na wiek – jedna grupa powyżej określonego wieku, druga poniżej tej wartości. W taki sposób wielu badaczy dzieli grupy i bierze pod uwagę inne istotne czynniki.

 

Co ciekawe mediana znalazła swoje zastosowanie nawet w grafice komputerowej i cyfrowym przetwarzaniu sygnałów. To m.in. dzięki niej pozbyliśmy się szumów na monitorach – mediana pozwala zachować ostre krawędzie przy jednoczesnej redukcji szumów. Mediana jest dużo bardziej odporna na elementy odstające niż średnia arytmetyczna, co przyczyniło się do tak szerokiego zastosowania wartości środkowej.