Miejscem zerowym funkcji określamy taki argument x, dla którego funkcja przyjmuje wartość zero. Aby lepiej zrozumieć tę definicję, warto powrócić do pojęć argumentu i wartości.

 

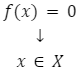
Argumenty znajdują się na osi poziomej układu współrzędnych i są to po prostu wszystkie x.

Wartości z kolei znajdują się na osi pionowej układu współrzędnych i są to y.

Odczytywanie miejsca zerowego na układzie współrzędnych

Odczytywanie miejsca zerowego z wykresu nie jest trudnym zadaniem. Wystarczy jedynie zwrócić uwagę, gdzie znajduje się punkt przecinający wykres funkcji z osią OX.

 

Istnieje kilka sposobów na przedstawienie funkcji. Jednym z nich jest tabelka. Nie musimy wcale przenosić funkcji na układ współrzędnych, aby odczytać jej miejsce zerowe. Dla przykładu zwróć uwagę na poniższą tabelkę:

 

x	1	4	8	32
f(x)	0	10	24	25

 

Z powyższej tabeli możemy odczytać, że miejscem zerowym tej funkcji jest x=1.

f(1)=0

Miejsce zerowe funkcji liniowej

Aby obliczyć miejsce zerowe funkcji liniowej, wystarczy jedynie porównać dany wzór funkcji do zera.

Przykład

f(x)=3x-9

Przyrównaj podaną funkcję do zera

3x-9=0

3x=9

Dzielimy obustronnie przez 3

x=3

Miejscem zerowym powyższej funkcji jest x=3.

Inne własności funkcji

Miejsce zerowe nie jest jedyną własnością funkcji. Oprócz niego istotne znaczenie mają również:

• dziedzina,
• zbiór wartości,
• monotoniczność,
• różnowartościowość,
• parzystość,
• nieparzystość,
• maksimum,
• minimum.

Dziedzina funkcji

Dziedziną funkcji nazywamy zbiór wszystkich argumentów danej funkcji. Dziedziną jest także zbiór x-ów, dla których została określona funkcja oraz zbiór x, dla których istnieje wykres funkcji. Dla każdej funkcji liniowej, kwadratowej, a także wielomianowej dziedziną jest zbiór liczb rzeczywistych. Określanie dziedziny funkcji jest potrzebne, aby uniknąć sytuacji, w której podstawiając do wzoru wartość liczbową, otrzymamy działanie, które jest niedozwolone w matematyce.

Zbiór wartości

Zbiorem wartości nazywamy wszystkie y, jakie funkcja może osiągnąć. Przy podanym wzorze funkcji możemy obliczyć wartość, jaką funkcja przyjmuje dla dowolnego argumentu x.

Monotoniczność

Z monotonicznością mamy do czynienia, kiedy funkcja jest rosnąca, malejąca lub stała, a także kiedy jest niemalejąca lub nierosnąca.

• kiedy wykres rośnie mamy do czynienia z funkcją rosnącą,
• kiedy wykres maleje, mamy do czynienia z funkcją malejącą,
• kiedy wykres rośnie lub jest stały, mamy do czynienia z funkcją niemalejącą,
• kiedy wykres maleje lub jest stały, mamy do czynienia z funkcją nierosnącą,

kiedy wykres jest linią poziomą, równoległą do osi OX, mamy do czynienia z funkcją stałą.