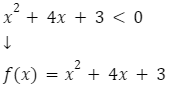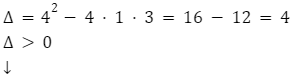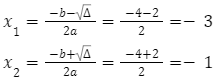Aby zrozumieć, czym są nierówności kwadratowe, warto powrócić do definicji równości kwadratowych. W tych drugich mamy do czynienia ze znakiem równości (=). W przypadku nierówności spotkamy znaki takie jak: <,≤,>,≥

Nierówności kwadratowe a równania kwadratowe – wzór

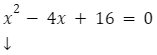
równanie kwadratowe,
występuje znak =

 

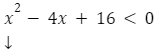
nierówność kwadratowa,
występuje znak  <

Nierówności kwadratowe a równania kwadratowe – rozwiązania

Obliczając równania kwadratowe, mogliśmy uzyskać jedno, dwa lub zero rozwiązań. Jak to wygląda w przypadku nierówności kwadratowych? Rozwiązaniem nierówności kwadratowej jest najczęściej przedział liczbowy.

 

Przykłady

Równanie kwadratowe:

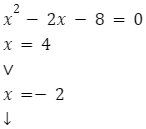
powyższe równanie kwadratowe ma dwa rozwiązania

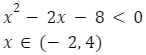
Rozwiązywanie nierówności kwadratowych

Aby rozwiązać nierówność kwadratową, wykonaj cztery poniższe kroki:

1. Przenieś wszystkie wyrazy na lewą stronę nierówności, tak aby po prawej stronie pozostało wyłącznie 0.
2. Lewa strona nierówności ma zostać rozwiązania tak samo jak wzór funkcji kwadratowej.
3. Obliczamy miejsca zerowe funkcji znajdującej się po lewej stronie – jeśli je posiada. Rysujemy jej wykres.
   Funkcja ma dwa miejsca zerowe
   

   
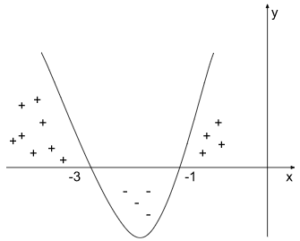
   Ramiona paraboli są skierowane do góry – współczynnik jest dodatni.

4. Odczytaj z wykresu rozwiązanie nierówności.
   Z powyższego rysunku wynika, że parabola przyjmuje wartości mniejsze od zera dla . Rozwiązaniem równania jest więc .

Rozwiązywanie równań kwadratowych

Wiesz już, w jaki sposób rozwiązywać nierówności kwadratowe. Jak to jednak jest w przypadku równań kwadratowych? Dlaczego równania kwadratowe są tak ważne w kontekście nierówności kwadratowych? Warto najpierw poznać te pierwsze, nauczyć się jak je rozwiązywać oraz jak rysować wykres funkcji kwadratowych. Dzięki temu obliczanie nierówności będzie dużo prostsze.

 

Równanie kwadratowe zapisujemy pod postacią wzoru:

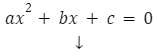a0
a,b,c R – współczynniki równania kwadratowego
x R  – zmienna

Sposób rozwiązania równania:

 

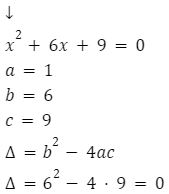
równanie ma jedno rozwiązanie:

 

Powyższe równanie ma jedno rozwiązanie:

 

Przykład:

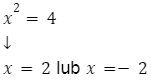
Rozwiązanie równania to lub

 

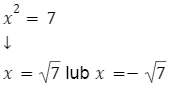
7 jest liczbą niewymierną, dlatego rozwiązane równanie pozostawiamy w postaci takiej, jaka została przedstawiona powyżej:

 

W zależności od wartości a, równanie kwadratowe może mieć:

• jedno rozwiązanie,
• dwa rozwiązania,
• nie mieć wcale rozwiązań.

 

1. jeśli , to równanie ma jedno rozwiązanie: ,
2. jeśli , to równanie ma dwa rozwiązania: i ,
3. jeśli , to równanie nie ma rozwiązania.