Objętość ostrosłupa obliczamy z wzoru:

 

Aby jednak móc prowadzić bezbłędne obliczenia, warto powrócić do najważniejszych właściwości ostrosłupa. Dzięki nim dowiemy się, w jaki sposób obliczyć pole podstawy, bo to właśnie ono jest ważnym elementem, bez którego nie obliczymy objętości.

Ostrosłup – definicja

Ostrosłupem nazywamy wielościan posiadający jedną podstawę i ściany boczne zbiegające się w jednym punkcie. Punkt ten określany jest wierzchołkiem. W podstawie ostrosłupa może znaleźć się dowolny wielokąt. Kiedy w podstawie znajduje się wielokąt foremny, wówczas ostrosłup określany jest prawidłowym.

 

Do najbardziej popularnych ostrosłupów prawidłowych zaliczamy:

• ostrosłup prawidłowy czworokątny,
• ostrosłup prawidłowy trójkątny.

Objętość ostrosłupa

Do obliczenia objętości ostrosłupa będziemy potrzebować nie tylko pola podstawy, ale także jego wysokości. Wzór na objętość prezentuje się następująco:

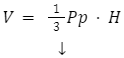V – objętość
Pp – pole podstawy ostrosłupa
H – wysokość ostrosłupa

Ostrosłup prawidłowy czworokątny

Ostrosłup prawidłowy czworokątny wyróżnia się na tle innych ostrosłupów swoją podstawą. Jest nią bowiem czworokąt foremny, czyli kwadrat. Ta specyficzna podstawa sprawia, że wierzchołek ostrosłupa prawidłowego czworokątnego leży dokładnie nad środkiem podstawy. Cechą charakterystyczną są jego cztery identyczne ściany boczne, będące trójkątami o równych długościach ramion, czyli trójkątami równoramiennymi.

 

Objętość ostrosłupa prawidłowego czworokątnego 

Podobnie jak z polem powierzchni całkowitej, wzór na objętość ostrosłupa prawidłowego czworokątnego również możemy wyprowadzić ze wzoru podstawowego:

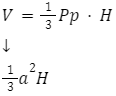
Ostrosłup prawidłowy trójkątny

Analogicznie, jak przy ostrosłupie prawidłowym czworokątnym w podstawie figury był czworokąt, tak w ostrosłupie prawidłowym trójkątnym znajduje się trójkąt równoboczny. W jego przypadku wierzchołek również leży dokładnie nad środkiem podstawy. Dzięki temu wszystkie trzy ściany boczne są takie same – są trójkątami równoramiennymi.

 

Wysokość (H) opuszczona z wierzchołka na podstawę leży na przecięciu dwusiecznych trójkąta równobocznego stanowiącego podstawę.

 

Objętość ostrosłupa prawidłowego trójkątnego

Wzór na objętość ostrosłupa prawidłowego trójkątnego po przekształceniu podstawowego wzoru możemy zapisać:

 

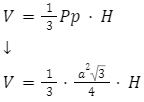
Pole powierzchni ostrosłupa prawidłowego trójkątnego 

Po przekształceniu podstawowego wzoru na pole powierzchni ostrosłupa możemy uzyskać wzór dla ostrosłupa prawidłowego trójkątnego. Po uwzględnieniu właściwości tej figury otrzymujemy następujący wzór: