Zanim przejdziemy do obliczania pola sześcianu, przypomnijmy sobie najważniejsze informacje o tym wielościanie. Dzięki temu sposób obliczania pola całkowitego będzie dla nas w pełni zrozumiały.

Sześcian – definicja

Sześcianem nazywamy wielościan foremny o sześciu ścianach, które są w kształcie przystających kwadratów. Jest jednocześnie szczególnym rodzajem prostopadłościanu. Pomiędzy ścianami sześcianu o wspólnej krawędzi znajduje się kąt prosty.

 

Sześcian posiada:

• 12 krawędzi,
• 8 wierzchołków,
• 4 przekątne.

 

Sześcian jest jednocześnie:

• graniastosłupem prawidłowym,
• hipersześcianem (w przestrzeni trójwymiarowej),
• prostopadłościanem,
• rombościanem.

Pole powierzchni sześcianu

Pole powierzchni całkowitej sześcianu obliczane jest poprzez dodanie wszystkich pól powierzchni ścian. Jako że wszystkie ściany sześcianu są takie same, wystarczy pole jednej ściany pomnożyć razy 6.

 

Wzór na pole powierzchni całkowitej sześcianu:

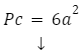a – bok sześcianu

 

Przykład 

Pole całkowite sześcianu wynosi . Jaka jest suma długości wszystkich krawędzi tego sześcianu?

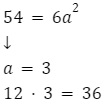
Suma długości wszystkich krawędzi tego sześcianu wynosi 36 m.

 

Sześcian – pozostałe wzory

Wzór na pole powierzchni nie jest jedynym wzorem, jaki warto zapamiętać w przypadku sześcianu. Jednak obliczanie poszczególnych wzorów sześcianu jest bardzo proste, ze względu na prostotę tej figury. Wszystkie ściany sześcianu mają bowiem taką samą powierzchnię, z kolei wszystkie krawędzie – taką samą długość.

 

Objętość sześcianu 

Do obliczenia objętości sześcianu potrzebujemy wyłącznie długość jednego boku. Wzór na objętość sześcianu wygląda następująco:

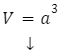a – bok sześcianu

Długość przekątnej sześcianu

Długość przekątnej sześcianu możemy obliczyć na dwa sposoby. Pierwszym z nich jest skorzystanie z gotowego wzoru, który wygląda następująco:

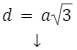d – przekątna sześcianu
a – bok sześcianu

 

W drugim sposobie na obliczenie długości przekątnej sześcianu korzystamy z twierdzenia Pitagorasa. Wystarczy wówczas zaobserwować, że w stworzonym trójkącie prostokątnym, w którym przeciwprostokątna jest przekątną sześcianu, przekątna podstawy to przekątna kwadratu, a więc: .

 

Promień kuli wpisanej w sześcian 

Zadania z kulą wpisaną w sześcian lub opisaną na sześcianie pojawiają się bardzo często. Warto więc poznać wzory na promień kuli wpisanej w sześcian i opisanej na sześcianie. Wzór na pierwszy, czyli promień kuli wpisanej w sześcian wygląda następująco:

Promień kuli opisanej na sześcianie 

Promień kuli opisanej na sześcianie zapisujemy z kolei wzorem: