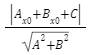Dwie proste możemy nazwać prostopadłymi, kiedy tworzą one kąty przyległe, a kąt przez nie utworzony ma miarę 90 stopni.

Ponadto dwie proste są do siebie prostopadłe, jeśli warunek: został spełniony przez dwie proste w postaci kierunkowej:

 

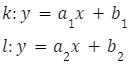
Dwie proste możemy także zapisać, wykorzystując postać ogólną. Wówczas:

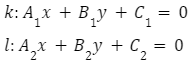
będą do siebie prostopadłe, jeśli zostanie spełniony następujący warunek:

 

Do oznaczenia prostych prostopadłych wykorzystujemy symbol:

Jak sprawdzić, czy proste są prostopadłe?

Sposób na sprawdzenie czy dane proste są prostopadłe względem siebie, przedstawiamy na poniższym przykładzie.

 

Przykład

Dane są proste:

oraz

Podstaw dane zgodnie z warunkiem:

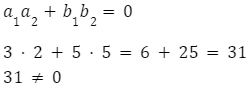
Powyższe proste nie są prostopadłe.

Proste prostopadłe a geometria analityczna

Pojęcie prostych prostopadłych pojawia się między innymi w geometrii analitycznej, która dotyczy figur znajdujących się w układzie współrzędnych. Aby lepiej zrozumieć definicję prostej prostopadłej, warto więc powrócić do najważniejszych pojęć związanych z układem współrzędnych. Jednym z najważniejszych zadań jest prawidłowe odczytywanie i zapisywanie współrzędnych punktów. A robimy to w następujący sposób:

4 – współrzędna x-owa
2 – współrzędna y-owa

 

Postać kierunkowa prostej

Postać kierunkową prostej zapisujemy następująco:

a – współczynnik kierunkowy prostej
b – druga współrzędna punktu, który przecina oś OY

 

Ważne: współczynnik kierunkowy prostej a jest równy tangensowi kąta nachylenia prostej względem osi OX.

Postać prostej w postaci ogólnej wygląda następująco:

 

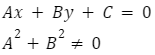
Proste równoległe na płaszczyźnie

Oprócz prostych prostopadłych na płaszczyźnie spotkamy się również z prostymi równoległymi.

 

Jeśli zostanie spełniony warunek , to

proste prostopadłe w postaci kierunkowej:

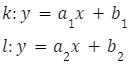
są równoległe.

Do oznaczenia prostych równoległych wykorzystujemy symbol: II

 

Proste równoległe mogą także występować w postaci ogólnej. Dla przykładu proste:

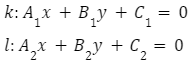
będą równoległe, jeśli zostanie spełniony następujący warunek:

Geometria analityczna – najważniejsze wzory

Para prostych:

Proste o równaniach kierunkowych: oraz mogą spełniać jeden z następujących warunków:

• są prostopadłe, kiedy:
• są równoległe, kiedy:

Prosta i punkt:

Odległość punktu od prostej określonej równaniem zapisujemy wzorem: