Równanie trygonometryczne to rodzaj równania, w którym niewiadomą jest argument funkcji trygonometrycznej.

Stosunki boków trójkąta prostokątnego

Funkcje trygonometryczne kąta ostrego, w trójkącie prostokątnym to stosunki długości boków tego trójkąta. Z ich stosowaniem mamy do czynienia nie tylko na lekcji matematyki, ale także w życiu codziennym. Warto więc się z nimi zapoznać.

 

1. W trójkącie prostokątnym stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej określamy sinusem kąta.
   
2. Cosinusem kąta nazywamy stosunek długości przyprostokątnej, która leży przy kącie do długości przeciwprostokątnej.
   
3. Tangensem kąta nazywamy stosunek długości przyprostokątnej, która leży naprzeciwko kąta do długości przyprostokątnej, która leży przy tym kącie.
   
4. Cotangensem kąta nazywamy stosunek długości przyprostokątnej, która leży przy tym kącie, do długości przyprostokątnej, która leży naprzeciwko kąta.

ctg =ca

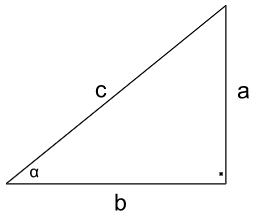
Wszystkie oznaczenia przyprostokątnych i przeciwprostokątnej, a także kąta znajdziesz na poniższym rysunku:

Przykład 1

Obliczanie wartości funkcji trygonometrycznej kąta 30° dla trójkąta równobocznego o boku długości 1.

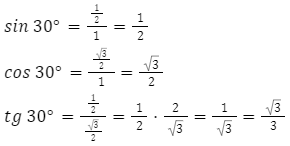
Przykład 2

Obliczanie funkcji trygonometrycznych dla kąta α, kiedy:

przyprostokątna b=3

przyprostokątna a=1

przeciwprostokątna c=

a kąt leży pomiędzy przeciwprostokątną c, a przyprostokątną b.

Obliczamy sinusa kąta :

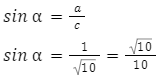
Obliczamy cosinusa kąta :

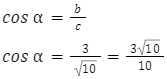
Obliczamy tangensa kąta :

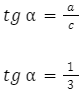
Tablice trygonometryczne

Tablice trygonometryczne okazują się niezbędne przy rozwiązywaniu równań trygonometrycznych.

Poniżej możesz zapoznać się z tabelą dokładnych wartości dla wybranych kątów. Z tablic trygonometrycznych możesz korzystać zarówno na lekcjach matematyki, jak i na egzaminie maturalnym.

 

	sin	cos	tg	ctg
0°	0	1	0	–
30°
45°			1	1
60°
90°	1	0	–	0
180°	0	-1	0	–
270°	-1	0	–	0
360°	0	1	0	–

 

Rozwiązywanie równań trygonometrycznych – zasada koła

Niektórzy do rozwiązywania równań trygonometrycznych wykorzystują zasadę koła. Dla wielu jest to jeden z prostszych sposobów na rozwiązywanie równań trygonometrycznych. Aby móc z niego korzystać należy m.in. znać tabelę znaków funkcji trygonometrycznych, która wygląda następująco.

 

	I	II	III	IV
sin	+	+	–	–
cos	+	–	–	+
tg	+	–	+	–
ctg	+	–	+	–

 

Aby łatwiej zapamiętać które funkcje trygonometryczne są dodatnie w poszczególnych ćwiartkach, uczniowie uczą się popularnej formułki:

“w pierwszej (ćwiartce) wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus”

Trygonometria – zastosowania

Wartości funkcji trygonometrycznych zależą jedynie od wielkości odpowiedniego kąta. Nie ma więc znaczenia wielkość trójkąta prostokątnego. To z kolei sprawia, że trygonometria odnajduje zastosowanie w życiu codziennym. To właśnie dzięki niej możliwe jest obliczenie wysokości wszelkiego rodzaju obiektów, kiedy obliczeń nie możemy dokonać bezpośrednio. Sprawdzi się nawet do obliczenia ile metrów siatki będzie potrzebnych, jeśli na bramę wjazdową należy zostawić określoną długość.