Prostymi równoległymi nazywamy dwie proste, które nie mają punktów wspólnych. Do oznaczania prostych równoległych wykorzystujemy symbol: II. W przypadku dwóch prostych na płaszczyźnie ich wzajemne położenie jest uzależnione od współczynników kierunkowych. Dwie proste nazwiemy więc równoległymi na płaszczyźnie, jeśli ich współczynniki kierunkowe a są równe.

 

Postać kierunkowa dwóch prostych równoległych:

dla

 

Przykład 

Dwie proste oraz

są równoległe, ponieważ ich współczynniki a są równe.

 

Postać ogólna dwóch prostych równoległych:

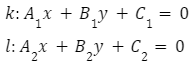
dla

Proste na płaszczyźnie – najważniejsze informacje

Proste równoległe nie są jedynymi prostymi, które możemy spotkać w układzie współrzędnych. Tuż obok nich równie istotne są proste prostopadłe. Czym z kolei są te proste?

 

Dwie proste możemy nazwać prostopadłymi, kiedy tworzą one kąty przyległe, a kąt przez nie utworzony ma miarę 90 stopni.

Ponadto dwie proste są to siebie prostopadłe jeśli warunek: został spełniony przez dwie proste prostopadłe w postaci kierunkowej:

 

Dwie proste prostopadłe możemy także zapisać, wykorzystując postać ogólną. Wówczas:

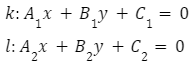
będą do siebie prostopadłe, jeśli zostanie spełniony następujący warunek:

 

Przykład

Dane są proste:

oraz

Podstawiamy dane zgodnie z warunkiem:

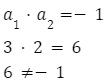
Powyższe proste nie są prostopadłe – iloczyn współczynników kierunkowych nie wynosi -1.

 

Do oznaczenia prostych prostopadłych wykorzystujemy symbol:

 

Prosta i punkt:

Odległość punktu od prostej określonej równaniem zapisujemy wzorem:

 

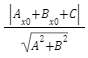
Para prostych:

Proste o równaniach kierunkowych: oraz mogą spełniać jeden z następujących warunków:

• są prostopadłe, kiedy:
• są równoległe, kiedy:

Proste prostopadłe i proste równoległe a geometria analityczna

Pojęcia prostych prostopadłych i prostych równoległych pojawiają się między innymi w geometrii analitycznej, która dotyczy figur położonych w układzie współrzędnych. Aby lepiej zrozumieć definicję prostej prostopadłej oraz prostej równoległej, warto powrócić do najważniejszych pojęć związanych z układem współrzędnych. Jednym z najważniejszych zadań, jakie należy opanować na samym początku, jest prawidłowe odczytywanie i zapisywanie współrzędnych punktów.

4 – współrzędna x-owa
2 – współrzędna y – owa