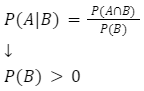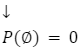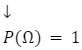Rachunek prawdopodobieństwa pozwala policzyć szansę wystąpienia jakiegoś zdarzenia.

 

Zdarzenie to może oznaczać, chociażby jaka jest szansa, że po rzucie kostką wypadnie 5 oczek. Jako że kostka ma sześć ścian i w rzucie może wypaść jedna z nich, co oznacza, że z sześciu możliwości oczekujemy jednej – wypadnięcia 5 oczek. Szansa na wypadnięcie ich wynosi więc rachunek prawdopodobieństwa 1.

Rachunek prawdopodobieństwa – pojęcia, które musisz znać

Zanim zapoznasz się ze sposobem obliczania rachunku prawdopodobieństwa, niezbędne będzie przyswojenie pojęć ściśle z nim związanych. Do najważniejszych zaliczamy:

  • zdarzenie elementarne,
  • doświadczenie losowe,
  • zdarzenie losowe,
  • moc zbioru,
  • zbiór wszystkich zdarzeń elementarnych.

 

Zdarzenie elementarne to wyłącznie jedno zdarzenie, które może się wydarzyć w doświadczeniu losowym – np. po rzucie kostką wypadły 3 oczka.

 

Doświadczeniem losowym  określamy daną czynność, którą wykonujemy – pozostając w temacie kostek do gry, doświadczeniem losowym będzie właśnie rzut kostką.

 

Zdarzeniem losowym określamy zbiór jednego bądź kilku zdarzeń elementarnych – przy rzucie kostką może być to np. wypadnięcie nieparzystej liczby oczek. Zdarzenie losowe oznaczamy symbolem A. Przy nieparzystej liczbie oczek dla rzutu kostką będzie to rachunek prawdopodobieństwa 2

 

Mocą zbioru określamy liczbę elementów wybranego zbioru. Dla zdarzenia losowego rachunek prawdopodobieństwa 2 mocą zbioru rachunek prawdopodobieństwa 3 będzie 3.

 

Zbiór wszystkich zdarzeń elementarnych to zbiór wszystkich zdarzeń elementarnych, które mogą się wydarzyć. Zbiór wszystkich zdarzeń elementarnych oznaczamy symbolem . Podczas rzutu kostką wszystkich zdarzeń może być 6, ponieważ kostka ma sześć ścian. Zbiór ten zapisujemy następująco rachunek prawdopodobieństwa 4

 

Przykład 

Rzucamy kostką. Jakie jest prawdopodobieństwo, że wypadnie liczba oczek mniejsza od 4?

Zdarzenie losowe: rzut kostką,

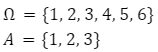
rachunek prawdopodobieństwa 5

Moce zbiorów:

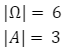
rachunek prawdopodobieństwa 6

Prawdopodobieństwo zdarzenia A:

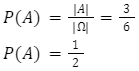
rachunek prawdopodobieństwa 7

Własności prawdopodobieństwa

  1. Prawdopodobieństwo zdarzenia niemożliwego wynosi 0.
    rachunek prawdopodobieństwa 8
  2. Prawdopodobieństwo zdarzenia pewnego wynosi 1.
    rachunek prawdopodobieństwa 9
  3. Prawdopodobieństwo wybranego zdarzenia losowego A zawsze będzie liczbą mieszczącą się w przedziale <0;1>
    rachunek prawdopodobieństwa 10

Prawdopodobieństwo całkowite

Dla wybranego zdarzenia A zachodzi wzór: rachunek prawdopodobieństwa 11

jeśli

rachunek prawdopodobieństwa 12 są zdarzeniami parami rozłączne oraz posiadają prawdopodobieństwa dodatnie, które możemy zsumować do jedynki.

Prawdopodobieństwo warunkowe

Wzór na prawdopodobieństwo zajścia zdarzenia A, jeśli zajdzie zdarzenie B obliczamy ze wzoru:

rachunek prawdopodobieństwa 13