Schematem Hornera nazywamy sposób obliczania wartości, dzięki któremu możliwe jest:

• dzielenie wielomianów przez dwumian x – a ,
• obliczenie wartości wielomianu dla danego argumentu,
• sprawdzenie, czy konkretna liczba stanowi pierwiastek wielomianu.

 

Schematu Hornera nie możemy wykorzystać, kiedy wielomian, przez który dzielimy, jest w wyższej potędze. W takiej sytuacji korzystamy z tradycyjnego sposobu na dzielenie wielomianów.

 

Do korzystania ze schematu Hornera niezbędna jest wiedza, jak prawidłowo tworzyć tabelę. Dzięki poniższemu przykładowi, algorytm Hornera stanie się dla Ciebie w pełni zrozumiały.

 

Tabela pozwalająca wykonywać algorytm Hornera składa się z dwóch wierszy. W górnym znajduje się współczynniki wielomianu, w dolnym z kolei wartość argumentu, dla którego liczymy wartość wielomianu.

 

Przykład

Dany jest wielomian:

Ma on zostać podzielony przez dwumian x+2, a dodatkowo mamy obliczyć wartość tego wielomianu dla argumentu x=-2

Pierwszym krokiem będzie prawidłowe sporządzenie tabeli. Pierwszy wiersz to współczynnik wielomianu. Jako że dzielimy przez dwumian x+2, to w drugim wierszu pod wielomianem W(x) znajdzie się -2.

 

W(x)	1	3	0	1	-3
-2	1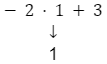

 

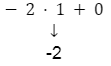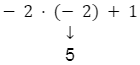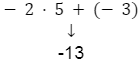Przy wpisywaniu kolejnych współczynników wielomianu należy pamiętać, że w tabelce musi zostać wpisane 0, jeśli nie ma kolejnej potęgi. Potęga ta istnieje, jednak ze współczynnikiem 0.

Schemat Hornera – o tym pamiętaj

Decydując się na wykorzystanie schematu Hornera, musisz pamiętać o kilku niezwykle istotnych ograniczeniach.

1. Kiedy stosujesz schemat Hornera przy dzieleniu wielomianów, wielomian musi być uporządkowany od najwyższej potęgi x.
2. Dwumian, przez który dzielisz, musi być zawsze stopnia pierwszego: x+b, x-b, gdzie b stanowi dowolną liczbę rzeczywistą.
3. Kiedy dzielisz dany wielomian przez dwumian stopnia wyższego niż pierwszy, nie możesz skorzystać z metody Hornera. Kiedy dwumian, przez który dzielisz, jest stopnia np. drugiego, wówczas możesz skorzystać z metody pisemnej dzielenia wielomianów.

Schemat Hornera – zastosowanie

Schemat Hornera jest szeroko wykorzystywany nie tylko na lekcjach matematyki, ale również w informatyce. To właśnie dzięki niemu możliwe jest zredukowanie mnożeń do jak najmniejszej ilości. Dzięki temu algorytmowi możliwe jest przeprowadzanie znacznie szybszych obliczeń wartości wielomianu.