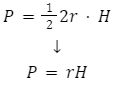Stożkiem nazywamy specyficzną bryłę ograniczoną przez powierzchnię stożkową. Obracając trójkąt prostokątny wokół jednej z przyprostokątnych, możemy otrzymać właśnie stożek. Przyprostokątna ta pełni jeszcze jedną istotną rolę dla stożka – jest ona jego wysokością. Druga z przyprostokątnych z kolei jest promieniem podstawy powstałej bryły. Tworząca stożka to z kolei przeciwprostokątna trójkąta prostokątnego.
Jako że stożek powstaje poprzez obrót trójkąta prostokątnego, nazywamy go bryłą obrotową.
Pole stożka
Na pole powierzchni całkowitej stożka składają się: pole podstawy i pole powierzchni bocznej. Wzór możemy więc zapisać następująco:
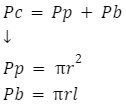
Wzór na pole całkowite to:
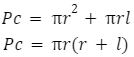
Pole powierzchni bocznej stożka
Powierzchnią boczną stożka jest wycinek koła o promieniu l i długości łuku 2r. Wzór na pole powierzchni bocznej:
Pole podstawy stożka
Stożek posiada w podstawie koło. Dlatego właśnie wcześniej wśród wzorów mogłeś zauważyć wzór na pole koła, czyli:
Objętość stożka
Do obliczenia objętości stożka potrzebujemy jego pola podstawy oraz wysokości. Jako że w podstawie stożka znajduje się koło, pole będziemy obliczać ze wzoru na pole koła, czyli 
.
Wzór na objętość stożka wygląda następująco:
Tworząca stożka
Tworzącą stożka nazywamy odcinek, który łączy dowolny punkt na okręgu podstawy z jego wierzchołkiem. Z definicji stożka możemy wywnioskować, że aby obliczyć długość tworzącej, musimy obliczyć długość przeciwprostokątnej w trójkącie prostokątnym, dzięki któremu ten stożek powstał.
Do obliczenia długości tworzącej stożka najlepiej wykorzystać twierdzenie Pitagorasa. Zgodnie z nim:
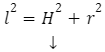l – tworząca stożka
H – wysokość stożka, oś obrotu,
r – promień podstawy stożka
Kąt nachylenia tworzącej stożka do płaszczyzny podstawy
Kątem nachylenia tworzącej stożka do płaszczyzny podstawy nazywamy kąt między przeciwprostokątną a jedną z przyprostokątnych w trójkącie prostokątnym, dzięki któremu powstał stożek. To oznacza, że możemy korzystać z poniższych wzorów:
Przekrój osiowy stożka
Przekrój osiowy stożka powstaje poprzez przecięcie bryły na dwie połowy przez jej środek i średnice podstawy. Dzięki takiemu działaniu uzyskamy w przekroju trójkąt równoramienny. Trójkąt ten będzie posiadał ramiona długości l i podstawę długości 2r.
Pole przekroju stożka
Do obliczenia pola przekroju osiowego stożka potrzebujemy długości boku trójkąta i jego wysokości. W tym przypadku wzór na pole powierzchni przekroju stożka będzie wyglądać:
