Twierdzenie cosinusów okazuje się niezwykle przydatne, kiedy znamy długości dwóch boków i miarę kąta znajdującego się między nimi. Dzięki niemu możemy obliczyć długość trzeciego boku, która jest nam nieznana.

 

Możemy powiedzieć, że twierdzenie cosinusów jest uogólnieniem twierdzenia Pitagorasa. W tym przypadku jednak trójkąt nie musi mieć miary kąta 90 stopni.

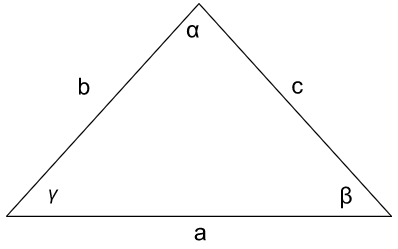
Korzystając z powyższych oznaczeń trójkąta, możemy zapisać następujący wzór zgodny  z twierdzeniem cosinusów:

 

Takie same zależności zachodzą przy pozostałych bokach:

 

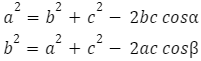
Kiedy mamy do czynienia z trójkątem prostokątnym, wzór ten sprowadza się do twierdzenia Pitagorasa. Wynika to z faktu, że cosinus kąta prostego wynosi 0.

 

Przykład

Dane są długości dwóch boków trójkąta a = 7, b = 5. Kąt między nimi wynosi 60 stopni.

Zgodnie z twierdzeniem cosinusów możemy zapisać:

 

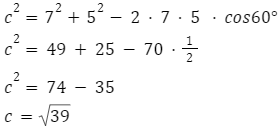
W dalszej kolejności obliczamy kąty, także na podstawie twierdzenia cosinusów, podstawiając do wzoru dane, które już posiadamy – długości wszystkich boków.

 

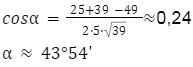
Aby upewnić się, że obliczenia zostały wykonane w prawidłowy sposób, należy zsumować wszystkie miary kątów. Suma miar kątów  w każdym trójkącie wynosi 180 stopni. Upewnij się, że wszystkie kąty po dodaniu pozwolą Ci uzyskać taki wynik.

Twierdzenie cosinusów w życiu codziennym

Choć możemy nie zdawać sobie z tego sprawy, trygonometria pojawia się w wielu dziedzinach naszego życia, gdy konieczne jest dokonanie różnych obliczeń. Twierdzenie cosinusów możemy odnaleźć chociażby w branży geodezyjnej czy budowlanej. To właśnie dzięki niemu możliwe jest dokonanie wszelkich obliczeń i pomiarów, w szczególności, gdy mamy do czynienia z dużym obiektem, którego nie możemy realnie zmierzyć. Posiłkowanie się twierdzeniem cosinusów pozwala uzyskać precyzyjne pomiary. Oprócz twierdzenia cosinusów możemy także korzystać z twierdzenia sinusów, które dotyczy zależności między bokami i kątami dowolnego trójkąta. Zgodnie z nim stosunek długości dowolnego boku do sinusa kąta, który leży naprzeciw tego boku, jest stały i równa się długości średnicy okręgu, który został opisany na tym trójkącie.