Twierdzenie sinusów możemy zastosować przy dowolnym trójkącie. Dotyczy ono zależności między bokami i kątami tego trójkąta.

 

Zgodnie z twierdzeniem sinusów, stosunek długości boku w dowolnym trójkącie do sinusa kąta leżącego naprzeciw tego boku jest stały, a także równy średnicy okręgu, który został opisany na tym trójkącie. Zgodnie z twierdzeniem możemy wyprowadzić następujący wzór:

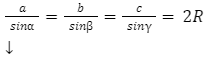
a, b, c – boki trójkąta wpisanego w okrąg
R – promień okręgu opisanego na trójkącie

 

Dzięki twierdzeniu sinusów możemy udowodnić m.in.:

• twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie,
• twierdzenie tangensów.

Twierdzenie sinusów – dowód

Kiedy to kąt prosty, jego sinus wynosi 1,  z kolei bok a ma długość średnicy. Wniosek ten pochodzi z twierdzenia o kątach środkowych i wpisanych na tym samym łuku. Mając powyższe dane, możemy zapisać:

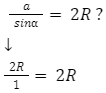
Powyższe twierdzenie jest prawdziwe.

 

Pozostałe twierdzenia

Twierdzenie sinusów nie jest jedynym twierdzeniem odnoszącym się do zależności między kątami i bokami trójkąta. Jednym z równie często spotykany jest twierdzenie cosinusów.

 

Twierdzenie cosinusów

Twierdzenie cosinusów okazuje się niezwykle przydatne, kiedy znamy długości dwóch boków i miarę kąta znajdującego się między nimi. Dzięki niemu możemy obliczyć długość trzeciego boku, który jest nam nieznany.

 

Możemy powiedzieć, że twierdzenie cosinusów jest uogólnieniem twierdzenia Pitagorasa. W tym przypadku jednak trójkąt nie musi mieć miary kąta 90 stopni.

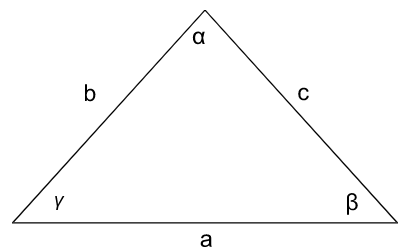
Korzystając z powyższych oznaczeń trójkąta, możemy zapisać następujący wzór zgodny  z twierdzeniem cosinusów:

Takie same zależności zachodzą przy pozostałych bokach:

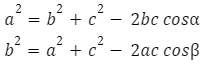
Kiedy mamy do czynienia z trójkątem prostokątnym wzór ten sprowadza się do twierdzenia Pitagorasa. Wynika to z faktu, że cosinus kąta prostego wynosi 0.

 

Przykład 

Dane są długości dwóch boków trójkąta a = 7, b = 5. Kąt między nimi wynosi 60 stopni.

Zgodnie z twierdzeniem cosinusów możemy zapisać:

 

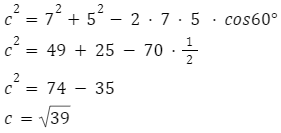
W dalszej kolejności obliczamy kąty także na podstawie twierdzenia cosinusów, podstawiając do wzoru dane, które już posiadamy – długości wszystkich boków.

 

 

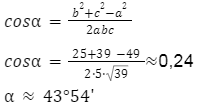
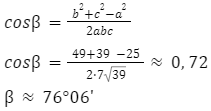
Aby upewnić się, że obliczenia zostały wykonane w prawidłowy sposób, należy zsumować wszystkie miary kątów. Suma miar kątów w każdym trójkącie wynosi 180 stopni – sprawdź czy wszystkie kąty po dodaniu dają taki wynik.