Twierdzenie Talesa należy do jednych z podstawowych twierdzeń pojawiających się w geometrii euklidesowej. Jak możemy wywnioskować z jego nazwy, sformułowanie twierdzenia jest przypisywane Talesowi z Miletu. Według niego:
Przecięcie kąta prostymi równoległymi sprawi, że stosunki odpowiednich otrzymanych odcinków będą równe.
Twierdzenie Talesa jest także ściśle powiązane z podobieństwem trójkątów. Oba te sposoby zapisywania stosunków odcinków możemy stosować zamiennie.
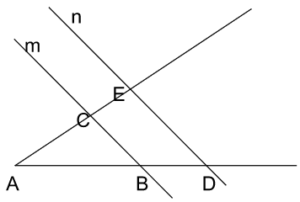
Na powyższym rysunku kąt został przecięty dwiema prostymi równoległymi względem siebie: m i n. Zgodnie z twierdzeniem Talesa zachodzą następujące proporcje:

Te same warunki zachodzą także w sytuacji, gdy proste równoległe przecinają kąty wierzchołkowe. Kątami wierzchołkowymi z kolei nazywamy dwa kąty posiadające wspólny wierzchołek. Oprócz tego przedłużeniem ramion jednego kąta są ramiona drugiego kąta.
Twierdzenie Talesa a podobieństwo trójkątów
- Dwa trójkąty są do siebie podobne, jeśli długości dwóch dowolnych boków jednego z nich są proporcjonalne do odpowiednich długości boków drugiego trójkąta. Kąty zawarte między tymi bokami muszą być sobie równe.
- Dwa trójkąty będą do siebie podobne, jeśli trzy boki jednego z nich są proporcjonalne do odpowiadających im boków drugiego trójkąta.
- Dwa trójkąty będą do siebie podobne, jeśli kąty jednego z nich będą odpowiednio równe kątom drugiego.
Twierdzenie Talesa w życiu codziennym
Twierdzenie Talesa okazuje się niezwykle przydatne w wielu sytuacjach. Jedną z nich jest konieczność dokonania pomiaru budynków lub innych obiektów wzniesionych na Ziemii. Z jego pomocą możemy obliczyć, chociażby wysokość lotu samolotu pasażerskiego. Co ciekawe sam Tales wykorzystywał swoje twierdzenie w praktyce. Z jego pomocą mierzył wysokość piramidy egipskiej oraz odległość statku od portu. Tales na własnych przykładach udowodnił poprawność twierdzenia, którego dzisiaj w żaden sposób nie moglibyśmy podważyć.
Choć obecnie korzystanie z twierdzenia Talesa przychodzi nam z łatwością i nie zachwycamy się proporcjonalnością odcinków powstałych na ramionach kąta z przecięcia dwóch prostych równoległych, w czasach samego Talesa, przyjęte przez niego założenie wywołało ogromne wrażenie. Warto więc zapamiętać wszystkie proporcje, które powstają po przecięciu prostymi równoległymi kąta, aby nie tylko łatwiej i szybciej dokonywać obliczeń w szkole, ale korzystać z nich także po jej ukończeniu. Wbrew pozorom, jest to jedno z niewielu Twierdzeń, które ułatwią nam życie codzienne.
