Ciąg geometryczny występuje również pod nazwą postęp geometryczny. Jest ciągiem liczbowym, w przypadku którego każdy kolejny wyraz – zaczynając od drugiego – jest iloczynem wyrazu poprzedniego, a także pewnej stałej. Stałą tę nazywamy ilorazem ciągu. Warto także zaznaczyć, że ciąg geometryczny może być skończony lub nieskończony.
Każdy wyraz ciągu geometrycznego będzie średnią geometryczną wyrazów sąsiednich, wyłączając jednak pierwszy i ostatni wyraz (jeśli ciąg jest skończony).
Aby w pełni zrozumieć, czym jest ciąg geometryczny, warto na chwilę powrócić do definicji samego ciągu. Możemy bowiem spotkać się nie tylko z ciągiem geometrycznym, ale także np. ciągiem arytmetycznym.
Ciąg liczbowy to nic innego jak ciąg liczb, który zazwyczaj powstaje zgodnie z określoną regułą. Reguła ta nie zawsze musi występować – ciąg liczb może istnieć bez niej – jednak tego rodzaju ciągi nie mają po prostu zastosowań. Ciągiem możemy nazwać także dowolną funkcję, której argumenty stanowią liczby naturalne.
Wzór ogólny ciągu
Wiedząc, że ciąg jest funkcją, możemy skorzystać ze wzoru: ![]() , dla
, dla ![]() . Znacznie prostszym i krótszym zapisem jest jednak:
. Znacznie prostszym i krótszym zapisem jest jednak: ![]() i to z nim spotykamy się najczęściej.
i to z nim spotykamy się najczęściej.
Ciąg geometryczny – wzory
Wzór na n-ty wyraz ciągu geometrycznego zapisujemy następująco:
![]()
lub:
![]()
Wzór na sumę n wyrazów ciągu zapisujemy następująco:
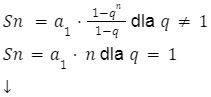
q – iloraz ciągu geometrycznego
Przykład
1,2,4,8,16,32,…,256
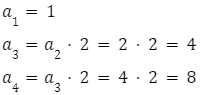
![]()
Iloraz dwóch kolejnych wyrazów powyższego ciągu geometrycznego wynosi 2.
Monotoniczność ciągu geometrycznego
Każdy ciąg geometryczny o dodatnim ilorazie jest monotoniczny. Kiedy pierwszy wyraz jest liczbą dodatnią, a iloraz:
- = 0, ciąg będzie stały i zbieżny do zera,
- = 1, ciąg będzie stały i zbieżny do pierwszego wyrazu,
- = -1, ciąg będzie naprzemienny, rozbieżny (jego granicami górnymi i dolnymi będą dwa pierwsze wyrazy),
- > 1, wyrazy ciągu będą rosnąć wykładniczo, ciąg będzie rozbieżny do nieskończoności,
- < -1, moduły wyrazów ciągu będą rosnąć wykładniczo, ciąg będzie rozbieżny,
- > 0 i < 1, wyrazy będą maleć wykładniczo, ciąg będzie zbieżny do zera,
- < 0 i > -1, wyrazy będą maleć wykładniczo, ciąg będzie zbieżny do zera.
Ciągi w życiu codziennym
Choć na co dzień możemy ich nie dostrzegać, ciągi pojawiają się w wielu dziedzinach naszego życia. Mamy z nimi do czynienia nie tylko w matematyce czy branży informatycznej, ale także np. w finansach. Także działanie naszych sprzętów – laptopów czy telefonów opiera się o ciągi geometryczne.
