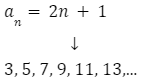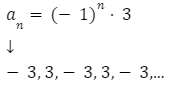Wyobraź sobie kolejno ustawione po sobie obiekty – możemy je nazwać ciągiem obiektów. Podobnie jest z ciągami liczbowymi. Jest to rodzaj ciągów, w których kolejne wyrazy stanowią liczby.

 

Wyróżniamy nie tylko ciągi liczbowe, ale także np.:

• ciąg prostych,
• ciąg wielokątów.

 

Przykłady:

1. Ciąg kwadratów kolejnych liczb naturalnych dodatnich:
2. Ciąg kolejnych przybliżeń
3. Ciąg naprzemienny liczb dodatnich i ujemnych:

Wszystkie powyższe ciągi powstawały zgodnie z ustaloną regułą.

 

Wyrazy ciągu

Wyrazami ciągu są kolejne liczby w ciągu, które powstały zgodnie z ustaloną regułą. Dla ciągu liczb trójkątnych: 1,3,6,10,15 wyrazami ciągu są kolejno liczby: 1, 3, 6, 10, 15.

 

Ważne: Każda funkcja, którą dziedziną jest zbiór liczb naturalnych dodatnich, jest ciągiem nieskończonym. Możemy jednak spotkać także ciągi skończone, których dziedziną jest zbiór skończony – ciąg: to ciąg n-wyrazowy.

Ciąg – sposoby określania ciągu

Ciągi możemy opisać na różne sposoby. Jednym z najczęściej spotykanych jest posiłkowanie się wzorem ogólnym ciągu. Wzór ten pozwala obliczyć wartość dowolnego wyrazu dla tego ciągu.

 

Przykładowe wzory ogólne ciągów:

1. 
2. 

 

Monotoniczność ciągu

Kiedy ciąg jest rosnący, malejący lub stały możemy go nazwać ciągiem monotonicznym.

 

• Ciąg jest ciągiem rosnącym, jeśli dla każdej liczby zostanie spełniona nierówność
• Ciąg jest ciągiem malejącym, jeśli dla każdej liczby zostanie spełniona nierówność

 

• Ciąg jest ciągiem stałym, jeśli wszystkie wyrazy ciągu są równe.

 

• Ciąg jest ciągiem malejącym, jeśli dla każdej liczby zostanie spełniona nierówność
• Ciąg jest ciągiem niemalejącym, jeśli dla każdej liczby zostanie spełniona nierówność
• Ciąg jest ciągiem nierosnącym, jeśli dla każdej liczby zostanie spełniona nierówność

Ważne: Każdy ciąg rosnący będzie ciągiem niemalejącym. Podobnie każdy ciąg malejący będzie ciągiem nierosnącym.

Badanie monotoniczności ciągu

Aby udowodnić, że dany ciąg jest rosnący, należy udowodnić, że dla każdego n zachodzi:

 

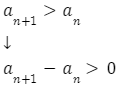
Analogicznie tak samo działamy, kiedy chcemy udowodnić, że ciąg jest malejący, stały, niemalejący czy nierosnący.

 

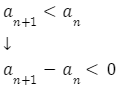
Przykład 

Należy wykazać, że ciąg jest rosnący

W pierwszej kolejności należy wyznaczyć wyraz

Następnie należy wyznaczyć różnicę

Z powyższego wynika, że co oznacza, że ciąg ten jest ciągiem rosnącym.