Termin dziedziny funkcji odnosi się do zbioru wszystkich argumentów funkcji. Aby lepiej zrozumieć definicję, warto powrócić do pojęć takich jak argument funkcji oraz wartość funkcji.

 

Argumenty funkcji to wszystkie x, czyli punkty z poziomej osi układu współrzędnych.

Wartościami funkcji są z kolei wszystkie y, czyli punkty z osi pionowej układu współrzędnych.

 

Dziedziną możemy nazwać zbiór x, dla którego określona jest funkcja oraz dla których istnieje wykres funkcji.

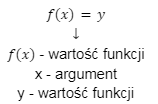
– wartość funkcji

x – argument

y – wartość funkcji (to samo co f(x) )

Wyznaczanie dziedziny funkcji

Wyznaczanie dziedziny funkcji ma najczęściej na celu wyeliminowanie sytuacji, w których pojawiają się argumenty, dla których musimy wykonać niedozwolone działanie, jak np. dzielenie przez 0.

 

Oprócz tego dzięki wyznaczaniu dziedziny funkcji unikamy:

• wyciągania pierwiastka parzystego stopnia z liczby ujemnej,
• logarytmowania liczby ujemnej,
• zapisywania w podstawie logarytmu liczby ujemnej bądź równej 1.

 

Najczęstsze działania niedozwolone, z którymi możemy się spotkać, to dzielenie przez 0 oraz wyciąganie pierwiastka z liczby ujemnej. Należy więc wyznaczać dziedzinę funkcji, aby uniknąć ryzyka podstawienia do wzoru wartości liczbowej, przez którą otrzymamy działanie niedozwolone w matematyce.

 

Dziedzinę funkcji można także odczytać z wykresu. Należy wówczas zwrócić uwagę, w jakiej części osi X leżą punkty wykresu. Warto także znać oznaczenia nanoszone na wykresie. Jeśli punkt został oznaczony pustym kółkiem, oznacza to, że nie należy on do dziedziny. Jeśli kółko naniesione na wykresie jest zamalowane, znaczy to, że punkt oznaczony w taki sposób należy do dziedziny.

Rodzaje funkcji a dziedzina

Do najczęściej spotykanych rodzajów funkcji zaliczamy:

• funkcję liniową,
• funkcję kwadratową,
• funkcję wielomianową,
• funkcję wykładniczą,
• funkcję wymierną.

Jak wygląda dziedzina dla każdej z tych funkcji?

 

Funkcja liniowa   

Dla funkcji liniowych dziedziną jest zbiór liczb rzeczywistych.

 

Funkcja kwadratowa 

Dla funkcji kwadratowych dziedziną jest zbiór liczb rzeczywistych.

 

Funkcja wielomianowa 

Dla funkcji wielomianowych dziedziną jest zbiór liczb rzeczywistych.

 

Funkcja wykładnicza 

Dla funkcji wykładniczych dziedziną jest zbiór liczb rzeczywistych.

 

Funkcja wymierna 

Dla funkcji wymiernych dziedziną jest zbiór liczb rzeczywistych z wyłączeniem takich x, które zerują mianownik.