Logarytm przedstawiamy za pomocą wzoru:
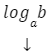 a – podstawa logarytmu
a – podstawa logarytmu
b – liczba logarytmowana
Dokonanie obliczeń nie jest trudne. Wystarczy jedynie zastanowić się, do jakiej potęgi należy podnieść liczbę a, by otrzymać liczbę b.
Aby logarytm mógł istnieć, muszą zostać spełnione trzy warunki:
- podstawa logarytmu to liczba dodatnia: a>0,
- podstawa jest różna od 1: a
 1
1 - liczba logarytmowana jest dodatnia: b>0
Metoda obliczania logarytmów
Aby obliczyć logarytm, równanie ![]() , wystarczy przekształcić na:
, wystarczy przekształcić na:
![]()
Z przekształconego równania należy następnie obliczyć liczbę x
Przykłady logarytmów
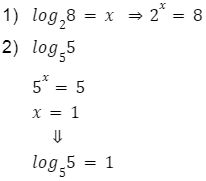
Logarytmy – wzory
Aby szybko dokonywać obliczeń, warto poznać najważniejsze wzory. Dotyczą one:
- dodawania logarytmów o tej samej podstawie,
- odejmowania logarytmów o tej samej podstawie,
- wyciągania wykładnika przed logarytm.
Jeżeli:
to mamy do czynienia z następującymi wzorami:
 – dodawanie logarytmów o tej samej podstawie
– dodawanie logarytmów o tej samej podstawie – odejmowanie logarytmów o tej samej podstawie
– odejmowanie logarytmów o tej samej podstawie – wyciąganie wykładnika potęgi przed logarytm
– wyciąganie wykładnika potęgi przed logarytm – logarytm w wykładniku potęgi
– logarytm w wykładniku potęgi – dzielenie logarytmów o tej samej podstawie
– dzielenie logarytmów o tej samej podstawie
Dodawanie i odejmowanie logarytmów
Dwa logarytmy posiadające taką samą podstawę możemy zarówno dodawać, jak i odejmować korzystając z poniższych wzorów:
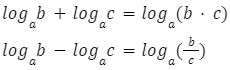
Przykład dodawania:
![]()
Przykład odejmowania:
![]()
Logarytm w wykładniku potęgi
Aby obliczyć potęgi z logarytmem w wykładniku, możemy skorzystać ze wzoru![]()
Przykład:
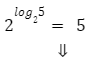 Zarówno podstawa całej potęgi, jak i podstawa logarytmu są równe 2, co oznacza, że cała potęga jest równa liczbie logarytmowanej, czyli liczbie 5.
Zarówno podstawa całej potęgi, jak i podstawa logarytmu są równe 2, co oznacza, że cała potęga jest równa liczbie logarytmowanej, czyli liczbie 5.
Wyciąganie wykładnika potęgi przed logarytm
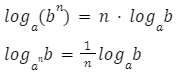
Przykład:
![]()
Logarytmy – zastosowanie
Ze względu na to, że logarytm jest funkcją odwrotną do funkcji wykładniczej, przydaje się tam, gdzie rozwiązywane są równania wykładnicze. Okazują się więc idealnym sposobem m.in. na obliczenie przyszłych liczb rat kredytu. Logarytmy są wykorzystywane także:
- w dziedzinach chemii np. do obliczania pH roztworu wodnego związku chemicznego (pH = – log [H+]),
- do obliczania poziomu natężenia dźwięku. Skala natężenia dźwięku opiera się bowiem na logarytmicznej jednostce miary Bel,
- w sejsmologii do obliczania wielkości trzęsienia ziemi przy wykorzystaniu skali logarytmicznej Richtera.
Przykładowe zadania z naszego kursu:
Więcej zadań można obejrzeć kupując nasz kurs tutaj.
str 105 zad 1
str 105 zad 2
