Pierwiastkowanie i potęgowanie wykorzystujemy nie tylko na lekcjach matematyki, ale także w życiu codziennym. Dowiedz się więc, na czym polegają oba te działania, a także poznaj najważniejsze wzory ułatwiające dokonywanie obliczeń. Poniżej przedstawiamy Ci zarówno definicję pierwiastkowania oraz potęgowania, jak i przykłady pozwalające je zrozumieć. Dowiesz się także z nich, jak wyglądają podstawowe działania na potęgach i pierwiastkach.

Pierwiastki

Pierwiastek kwadratowy z liczby nieujemnej a, to liczba nieujemna b, której kwadrat wynosi a:

kiedy oraz

 

 

Przykład

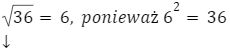
Chociaż , to nie jest równy 6. Wynika to  samej definicji pierwiastka kwadratowego, która mówi nam, że pierwiastek kwadratowy jest liczbą nieujemną.

 

Pierwiastek sześcienny – inaczej trzeciego stopnia – z liczby nieujemnej a jest taką liczbą b, która podniesiona do trzeciej potęgi pozwoli nam uzyskać liczbę a:

kiedy

 

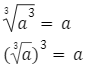
Obliczanie pierwiastka trzeciego stopnia to działanie odwrotne do podnoszenia do trzeciej potęgi.

 

Przykłady

• 
• 

 

Ważne: wynikiem pierwiastkowania zawsze musi być liczba dodatnia. Pod pierwiastkiem także może znaleźć się wyłącznie liczba dodatnia.

Działania na pierwiastkach

Pierwiastek iloczynu:

 

Przykład:

Pierwiastek iloczynu równa się iloczynowi pierwiastków.

 

Pierwiastek ilorazu:

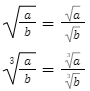
Potęgi

Potęgi służą do zapisywania długich iloczynów w prostszy sposób. Na potęgach mogą być wykonywane różne działania, z którymi zapoznasz się poniżej.

Zapis potęgi:

a – podstawa potęgi
n – wykładnik potęgi

 

Potęga to iloczyn n czynników równych liczbie a dla liczby naturalnej n>1

Ważne: Nie definiujemy wartości .

 

Warto znać także niektóre potęgi liczb: 2, 3, 4, 5 co przyspiesza wiele obliczeń.

 

n
1	2	3	4	5
2	4	9	16	25
3	8	27	64	125
4	16	81	256	625
5	32	243	1024
6	64	729
7	128
8	256
9	512
10	1024

 

Przykład

• 
• 
• 

 

Podczas obliczania wartości wyrażeń, w których występują potęgi, warto korzystać z prawa działania na potęgach:

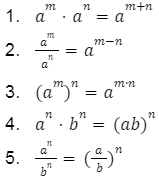
Potęgowanie i pierwiastkowanie – najważniejsze wzory

Wzory na potęgi o wykładnikach wymiernych: 

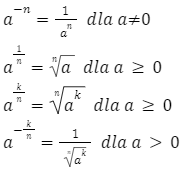
Potęgowanie i pierwiastkowanie w życiu codziennym

Wiedza o potęgach i pierwiastkach jest potrzebna nie tylko w szkole. Korzystamy z niej także w późniejszym życiu, chociażby do obliczania powierzchni danego pomieszczenia. Dzięki temu możemy dowiedzieć się, ile materiału potrzebujemy do przeprowadzenia remontu w danym pokoju.