Równania kwadratowe – czym są?
Zapoznając się ze specyfiką równań kwadratowych, warto powrócić do wiedzy o równaniach liniowych. W przypadku równań liniowych niewiadoma x występuje zawsze w pierwszej potędze. Inaczej jest w przypadku równań kwadratowych – tutaj niewiadoma x występuje w drugiej potędze – ![]() . Współczynniki równania kwadratowego są nazywane kwadratowymi, liniowymi i stałymi.
. Współczynniki równania kwadratowego są nazywane kwadratowymi, liniowymi i stałymi.
Ważne: Równanie kwadratowe może wystąpić również pod nazwą: równanie drugiego stopnia.
Aby obliczyć równanie kwadratowe, należy wyznaczyć wszystkie liczby, spełniające dane równanie. W praktyce oznacza to, że należy odszukać liczby, które po podstawieniu pod x pozwolą uzyskać równość prawdziwą.
Równanie kwadratowe może mieć:
- jedno rozwiązanie,
- dwa rozwiązania,
- nie mieć rozwiązań wcale.
Przykłady równań kwadratowych:
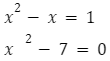
Rozwiązywanie równań kwadratowych
Sposób rozwiązania równania: ![]()
![]()
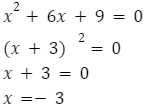
Powyższe równanie ma jedno rozwiązanie: ![]()
Rozwiązanie równania kwadratowego występują również pod nazwą pierwiastki równania kwadratowego.
Równania kwadratowe w postaci ogólnej
Postać ogólna równania kwadratowego wygląda następująco:
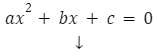 a, b, c – współczynniki liczbowe
a, b, c – współczynniki liczbowe
a![]() 0
0
Do obliczania równania kwadratowego możemy wykorzystać wzór na deltę:
![]()
Równanie kwadratowe ma dwa rozwiązania jeśli ![]() , wówczas:
, wówczas:
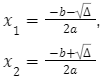
Równanie kwadratowe ma jedno rozwiązanie, jeśli ![]() , wówczas:
, wówczas:
![]()
Równanie kwadratowe nie ma rozwiązań, jeśli ![]()
Proste równania kwadratowe
Najprostszą formę równania kwadratowego możemy zapisać:
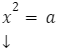
a – dowolna liczba rzeczywista
W zależności od wartości a, równanie to może mieć:
- jedno rozwiązanie,
- dwa rozwiązania,
- nie mieć wcale rozwiązań.
- jeśli
 , to równanie ma jedno rozwiązanie:
, to równanie ma jedno rozwiązanie: 
- jeśli
 , to równanie ma dwa rozwiązania:
, to równanie ma dwa rozwiązania:  i
i 
- jeśli
 , to równanie nie ma rozwiązania.
, to równanie nie ma rozwiązania.
Przykład:
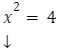
![]() lub
lub ![]()
Rozwiązanie równania to ![]() lub
lub ![]()
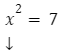
![]() lub
lub ![]()
7 jest liczbą niewymierną, dlatego rozwiązanie równanie pozostawiamy w postaci takiej, jaka została przedstawiona powyżej: ![]()
Równania, które można sprowadzić do równań kwadratowych
W przypadku równań dwukwadratowych istnieje możliwość przekształcenia na równania kwadratowe.
![]()
![]() t – nowa niewiadoma, t
t – nowa niewiadoma, t ![]() 0
0
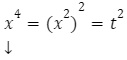
poprzez wykorzystanie nowej niewiadomej t, początkowe równanie możemy zapisać:
![]()
Gdy powyższe równanie będzie miało dwa rozwiązania, to korzystamy z równań
![]()
