Zanim przejdziemy do dwóch sposobów na rozwiązywanie układów równań, na chwilę powrócimy do samej definicji układów. Układem równań nazywamy złączenie przynajmniej dwóch równań. Mogą one składać się z większej liczby równań i większej liczby niewiadomych – nie tylko dwóch. Poniżej przedstawiamy Ci przykładowe układy równań:

 

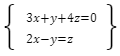
Na lekcjach matematyki możemy spotkać się z układem dwóch równań zawierających właśnie dwie niewiadome – x i y. Para liczb, która spełnia oba równania, jest nazywana rozwiązaniem równania. Istnieje kilka sposobów na rozwiązanie układów równań. Poniżej przedstawiamy Ci metodę:

• przez podstawianie,
• przeciwnych współczynników.

Metoda podstawiania

Podstawianie to sposób, w którym wyznaczamy z jednego równania jedną niewiadomą i podstawiamy ją do drugiego równania. Aby lepiej poznać ten sposób, zapoznaj się z poniższym przykładem.

 

Przykład

Dany jest układ równań:

 

Pierwszym krokiem będzie obliczenie x w pierwszym równaniu:

Kiedy wiesz już, ile wynosi x, możesz podstawić ją do drugiego równania. W ten sposób w drugim równaniu zostanie tylko jedna niewiadoma – y.

 

Teraz przyszedł czas na zajęcie się drugim równaniem i obliczenie y.

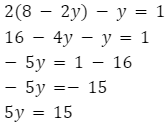
Znając wartość y możesz teraz obliczyć x:

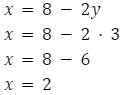
Z powyższych obliczeń wynika, że rozwiązaniem równania są:

x=2
y=3

Metoda przeciwnych współczynników

Kiedy przy tej samej niewiadomej w dwóch równaniach mamy przeciwne współczynniki, wówczas zgodnie z metodą przeciwstawnych współczynników, możemy dodawać równania stronami. Na poniższym przykładzie przedstawiamy Ci, jak to wygląda w praktyce:

 

Przykład

Dany jest układ równań:

 

Jest to ten sam układ równań, którym zajmowaliśmy się przy metodzie podstawiania. Możemy więc rozwiązać go na dwa sposoby.

 

Pierwszym krokiem będzie pomnożenie pierwszego równania, dzięki czemu przy niewiadomej y w obu równaniach znajdzie się 2.

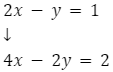
Otrzymujemy wówczas następujący układ równań:

 

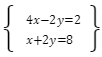
Teraz możemy dodać równania stronami, dzięki czemu otrzymujemy:

Z powyższego równania możemy obliczyć x:

Z dowolnego równania wystarczy obliczyć y. Nie ma znaczenia, czy wybierzemy pierwsze, czy drugie równanie z układu równań. Wystarczy w jednym z nich za x podstawić obliczoną wartość.

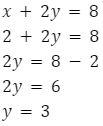
Z powyższych obliczeń wynika, że rozwiązaniem równania będzie:

x = 2
y = 3