Wartość bezwzględną możemy określić jako odległość liczby rzeczywistej x od zera. Jako że odległości nie możemy podawać w formie ujemnej, wartość bezwzględna każdej liczby zawsze będzie liczbą dodatnią.

 

Wartość bezwzględna liczby x wygląda:

Dla każdej liczby dodatniej wartością bezwzględną jest ta sama liczba dodatnia

Przykłady:

 

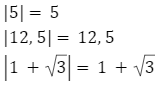
Dla liczb ujemnych wartością bezwzględną są liczby do nich przeciwne

Przykłady:

 

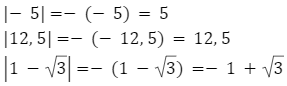
Dla zera wartość bezwzględna będzie równa zeru:

Wartość bezwzględna – własności

1. Gdy  wartością bezwzględną dowolnej liczby rzeczywistej x będzie ta sama liczba rzeczywista x.
2. Gdy  wartością bezwzględną dowolnej liczby rzeczywistej x będzie liczba przeciwna do x, czyli -x.
3. Definicja pierwiastka arytmetycznego, który zawsze jest nieujemny, mówi nam, że dla każdej liczby rzeczywistej x zachodzi:

 

Oprócz powyższych warto znać także własności:

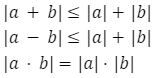
Wykres wartości bezwzględnej

Najprostszym sposobem na narysowanie wykresu wartości bezwzględnej jest sporządzenie tabeli, w której zaznaczymy wartości bezwzględne dla przykładowych wartości x. W praktyce wygląda to następująco:

 

	-4	-2	0	2	4
	4	2	0	2	4

 

Wystarczy teraz tylko zaznaczyć wyznaczone punkty na układzie współrzędnych i narysować wykres.

Wartość bezwzględna wyrażeń z x-em

Co jeśli wewnątrz wartości bezwzględnej znajduje się wyrażenie z x? Wówczas przy opuszczaniu wartości bezwzględnej należy rozpatrzyć dwa rozwiązania:

 

1. Musisz opuścić wartość bezwzględną bez zmiany znaku dla x, dla których wyrażenie pod wartością bezwzględną jest równe 0 lub jest większe od 0.
2. Musisz opuścić wartość bezwzględną ze zmianą znaku dla x, dla których wyrażenie pod wartością bezwzględną jest mniejsze od 0.

Równania z wartością bezwzględną

Posiadając równanie , wiemy, że to, co znajduje się pod wartością bezwzględną, musi być równe liczbie b bądź liczbie, która jest przeciwna do b, czyli -b. Opuszczając wartość bezwzględną, możemy otrzymać więc dwa równania:

lub

Po ich rozwiązaniu otrzymujemy:

lub

 

Przykład

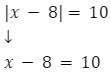
lub

Wartość bezwzględna – funkcje

Funkcja rzeczywistej wartości bezwzględnej jest ciągła w każdym punkcie. Funkcja ta maleje w przedziale (), a rośnie w przedziale (). Zarówno liczba rzeczywista, jak i liczba do niej przeciwna posiadają tę samą wartość bezwzględną, co oznacza, że wspomniana funkcja jest parzysta, a zarazem nieodwracalna.