Zanim przejdziemy do sposobu rysowania funkcji liniowej, powróćmy do podstawowych informacji na jej temat.

Funkcja liniowa

 

Wykres funkcji liniowej to linia prosta. Funkcję liniową przedstawiamy za pomocą wzoru:

funkcja - definicja i własności 3a – współczynnik kierunkowy prostej
b – wyraz wolny

 

Znacznie częściej możemy jednak spotkać się z zapisem:

funkcja - definicja i własności 4

Wykres funkcji liniowej to linia prosta.

Funkcja liniowa jest:

  • rosnąca, jeśli a>0,
  • stała, jeśli a=0,
  • malejąca, jeśli a<0.

Funkcja liniowa – wykres

Wykres funkcji liniowej to prosta, do której narysowania wystarczy wyznaczenie dwóch punktów, które do niej należą.

 

Przykład

Funkcja liniowa wykres funkcji liniowej 1

Aby narysować wykres funkcji, należy obliczyć współrzędne dwóch dowolnych punktów, przez które poprowadzona jest prosta.

 

Dla wykres funkcji liniowej 2
wykres funkcji liniowej 3
z tego wynika, że do wykresu funkcji należy punkt o współrzędnych (0,-1)

 

Dla wykres funkcji liniowej 4
wykres funkcji liniowej 5
z tego wynika, że do wykresu funkcji należy punkt o współrzędnych (2,3)

 

Posiadając współrzędne dwóch punktów, wystarczy zaznaczyć je na układzie współrzędnych i poprowadzić prostą przechodzącą przez nie.

Miejsce zerowe funkcji liniowej

Miejsce zerowe funkcji liniowej jest taką wartością argumentu, dla której wartość wynosi zero. Argumenty to wartości funkcji z poziomej osi układu współrzędnych: x.

 

Aby obliczyć miejsce zerowe funkcji liniowej, możesz porównać wzór funkcji do zera.

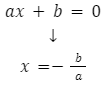
wykres funkcji liniowej 6

 

Przykład

Funkcja wykres funkcji liniowej 7

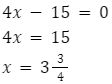
wykres funkcji liniowej 8

 

Funkcja liniowa ma:

  • jedno miejsce zerowe, kiedy przecina się z osią OX, aróżne od0,
  • nieskończoną ilość miejsc zerowych, kiedy zapisana jest równaniem a=0, b=0,
  • nie ma ani jednego miejsca zerowego, kiedy a=0, bróżne od0.

Proste równoległe i proste prostopadłe a funkcja liniowa

Proste o równaniach:

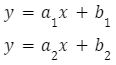
wykres funkcji liniowej 11

  • są prostymi równoległymi do siebie, jeśli ich współczynniki kierunkowe są takie same: wykres funkcji liniowej 12
  • są prostymi prostopadłymi, kiedy ich współczynniki kierunkowe spełniają podaną poniżej zależność:
    wykres funkcji liniowej 13

Funkcja liniowa w życiu codziennym

Zakres zastosowań funkcji liniowej jest bardzo szeroki. Tego rodzaju funkcja jest nieoceniona przy analizie dynamiki oraz współzależności. Możemy wykorzystać ją, chociażby do zbadania współzależności pomiędzy poziomem wykształcenia a pensją. Funkcja liniowa jest więc częścią statystyki. Odgrywa także istotną rolę w linearyzacji skomplikowanych zagadnień – w takim przypadku model układu liniowego pomaga przybliżyć model układu nieliniowego. Szerokie zastosowanie w życiu codziennym oznacza, że warto poznać i zapamiętać własności funkcji liniowej i sposób rysowania jej wykresu.