Aby zdefiniować ciąg rekurencyjnie, należy podać jego pierwszy wyraz i wzór pozwalający obliczyć wyraz ciągu na podstawie wyrazu n-tego.

 

Ciąg możemy więc określić poprzez:

• podanie wzoru ogólnego,
• podanie jego pierwszego wyrazu i reguły wyznaczania kolejnych wyrazów.

 

O zdefiniowaniu rekurencyjnym ciągu mówimy, jeśli:

• został określony skończony zbiór wyrazów tego ciągu – najczęściej jest to pierwszy wyraz ciągu bądź kilka pierwszych wyrazów,
• pozostałe wyrazy ciągu będą wyrażone przy użyciu poprzednich wyrazów danego ciągu.

 

Mając wzór ogólny ciągu, dużo prościej jest zapisać wzór rekurencyjny, niż wyznaczyć wzór ogólny ciągu, gdy znamy określenie rekurencyjne danego ciągu.

 

Wzór rekurencyjny możemy wyznaczyć różnymi sposobami, tak samo jak ma to miejsce w przypadku wyznaczania wzoru ogólnego ciągu.

Przykład 

Mając ciąg mówiący nam o tym, że dla każdej liczby naturalnej przyporządkowano jej kwadrat, możemy wyznaczyć dwa wzory rekurencyjne.

W pierwszej kolejności należy wyznaczyć pierwszy wyraz ciągu i wyraz

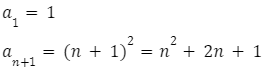
Następne na podstawie różnicy należy określić ciąg rekurencyjny

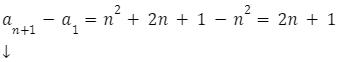
Wzór rekurencyjny wygląda następująco:

Aby otrzymać wzór rekurencyjny, możesz także obliczyć iloraz:

Dzięki temu otrzymujemy wzór rekurencyjny wyglądający następująco:

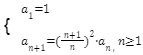
Ciąg Fibonacciego

Jednym z najbardziej znanych ciągów rekurencyjnych jest ciąg Fibonacciego. Jego nazwa pochodzi od nazwiska samego matematyka, który spotkał się z tym ciągiem podczas badania dynamiki rozmnażania populacji królików.

 

W przypadku ciągu Fibonacciego każdy kolejny wyraz jest sumą dwóch wyrazów, które go poprzedzają:

1+1+=2

1+2=3

2+3=5

3+5=8

…

 

Ciąg Fibonacciego pojawia się nie tylko w cyklu rozwojowym królików. Co ciekawe wiele obszarów w przyrodzie także się na nim opiera. Ciąg Fibonacciego ma, chociażby ścisły związek z ułożeniem ziaren słonecznika czy kształtem muszli łodzika.

Ciąg ten pojawia się także w zadaniach związanych z kombinatoryką. To właśnie on okazuje się pomocny, kiedy zastanawiamy się, na ile sposobów możemy wykonać konkretne zadanie, gdy posiadamy warunki ograniczające.