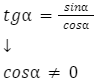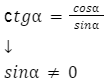Zanim zapoznasz się z najważniejszymi wzorami trygonometrycznymi, powróć na chwilę do samej definicji trygonometrii. Działem matematyki zajmującym się zależnościami między długościami boków a miarami kątów wewnętrznych w trójkącie nazywamy właśnie trygonometrią.
Najważniejsze informacje, jakie musisz zapamiętać z tego działu to:
- 4 funkcje trygonometryczne – sinus, cosinus, tangens i cotangens,
- te 4 funkcje działają na kątach,
- funkcje te definiuje się w trójkącie prostokątnym jako stosunki odpowiednich boków.
Najważniejsze wzory trygonometryczne
Między funkcjami trygonometrycznymi jednego kąta zachodzą następujące związki:
Wartości funkcji trygonometrycznych dla kątów ostrych odnajdziemy w tablicach.
Jedynka trygonometryczna
Wzór na jedynkę trygonometryczną to:
![]()
Tangens i cotangens
Wzory na tangens i cotangens to:
Podwójny kąt
Funkcje trygonometryczne dla podwojonego kąta to:
Funkcje trygonometryczne – sumy i różnice kątów
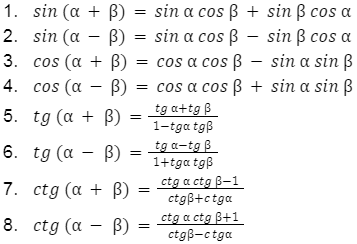
Wzory redukcyjne
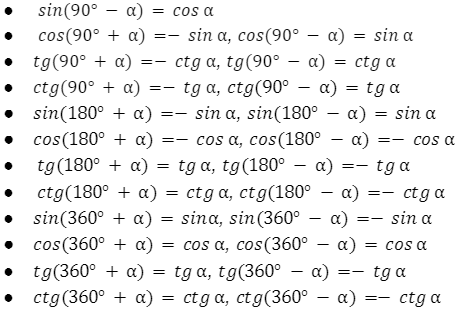
Iloczyn funkcji trygonometrycznych
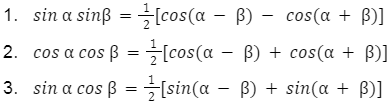
Różnice kwadratów funkcji trygonometrycznych
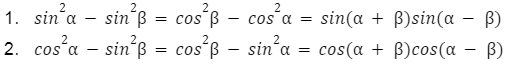
Trygonometria – zastosowanie
Trygonometria odnajduje swoje zastosowanie w wielu dziedzinach naszego życia. To właśnie dzięki niej możliwe jest obliczanie rzeczywistych wysokości nawet bardzo dużych obiektów. Do dokonania dokładnych pomiarów wystarczy nam zwykła miarka i kątomierz. To właśnie dzięki trygonometrii możliwe jest także działanie wszelkiego rodzaju urządzeń nawigacyjnych. Dzięki niej ogromny postęp został także odnotowany w badaniach astronomicznych. Trygonometria okazuje się także niezbędna w przetwarzaniu sygnałów.