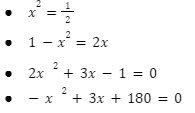Wzór na deltę
Wyróżnik trójmianu kwadratowego dużo częściej występuje pod pojęciem delta. Obie te nazwy możemy jednak stosować wymiennie. Wzór na deltę jest jednym z najważniejszych wzorów do zapamiętania, bez którego ciężko wyobrazić sobie działania na równaniach kwadratowych. Wzór na deltę to:
![]()
Równanie kwadratowe
Obliczenie równania kwadratowego to nic innego, jak wyznaczenie wszystkich liczb spełniających konkretne równanie. W praktyce oznacza to, że liczby, które podstawimy pod x, pozwolą nam otrzymać równość prawdziwą. Równanie kwadratowe nie musi mieć wyłącznie jednego rozwiązania – może mieć ich dwa lub nie mieć wcale. Rozwiązanie równania kwadratowego określane jest także pierwiastkiem równania kwadratowego.
Równanie kwadratowe zapisujemy pod postacią wzoru:
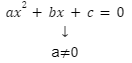
![]() – współczynnik równania kwadratowego
– współczynnik równania kwadratowego
![]() – zmienna
– zmienna
Wyróżnik równania kwadratowego
Wyróżnik równania kwadratowego to właśnie delta, której wzór warto zapamiętać na długo. Przydaje się on w wielu zadaniach i to nie tylko związanych z funkcją kwadratową.
Przykładowe równania kwadratowe:
Rozwiązanie równania kwadratowego
Wiesz już, że równanie kwadratowe może mieć jedno, dwa lub zero rozwiązań. Ich liczba uzależniona jest od wartości delty.
Jeśli:
 , to równanie kwadratowe będzie mieć dwa rozwiązania. Aby je obliczyć, musisz skorzystać z poniższych wzorów:
, to równanie kwadratowe będzie mieć dwa rozwiązania. Aby je obliczyć, musisz skorzystać z poniższych wzorów:
![]()
![]()
 , to równanie kwadratowe będzie mieć tylko jedno rozwiązanie. Aby je obliczyć, skorzystaj z wzoru:
, to równanie kwadratowe będzie mieć tylko jedno rozwiązanie. Aby je obliczyć, skorzystaj z wzoru:
![]()
Kiedy ![]() , pierwiastek
, pierwiastek ![]() nazywamy pierwiastkiem podwójnym.
nazywamy pierwiastkiem podwójnym.
 , to równanie kwadratowe nie będzie mieć żadnych rozwiązań.
, to równanie kwadratowe nie będzie mieć żadnych rozwiązań.
Przykład
Jakie jest rozwiązanie równania : 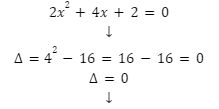
kiedy delta jest równa zero, oznacza to, że posiada jedno rozwiązanie. Korzystając z wzoru, możemy je obliczyć.
![]()
Rozwiązaniem równania jest -1
Zastosowanie Delty
W obliczeniach matematycznych wartość delty pozwala nam obliczyć miejsce zerowe funkcji kwadratowej bądź współrzędne wierzchołka paraboli. Współczynnik delty występuje jednak w znacznie większym obszarze nauk ścisłych. Bez obecności delty nie istniałby tak rozbudowany świat nauk fizycznych. Delta pojawia się między innymi w równaniu przewodnictwa cieplnego czy równaniu Helmoltza. Stanowi ona także ważną część mechaniki kwantowej. Z ciekawostek, które mogą cię zaskoczyć, imponujący może być fakt, że równania kwadratowe były rozwiązywane już w starożytności przez Babilończyków. Tabliczki klinowe pochodzące z ok. 1800 roku p.n.e. są tego jasnym dowodem.