Wzory skróconego mnożenia – czym są?
Głównym zadaniem wzorów skróconego mnożenia jest ułatwienie dokonywania szybszych obliczeń. Odgrywają istotną rolę przy znajdowaniu pierwiastków, przekształcaniu czy rozwiązywaniu równań. Do najczęściej wykorzystywanych wzorów skróconego mnożenia należą wzory na:

Warto zapoznać się z powyższymi wzorami i prześledzić sposób ich stosowania, aby w przyszłości ułatwić i skrócić czas rozwiązywania obliczeń. 8 powyższych wzorów pomaga doprowadzić wyrażenia algebraiczne do najprostszej postaci.
Kwadrat sumy
Wzór na kwadrat sumy pozwala na znaczące przyspieszenie obliczeń. Jego zapis to:
![]()
Wzór ten występuje także w wersjach dla większej liczby składników np.:
![]()
Wzór ten może być więc uniwersalnie stosowany dla kwadratu dowolnej liczby składników.
Kwadrat różnicy
W przypadku kwadratu różnicy mamy do czynienia z wzorem:
![]()
Tak samo jak przy kwadracie sumy, wzór ten może zostać wykorzystany nie tylko przy dwóch składnikach, ale przy dowolnej ich ilości.
Przykłady
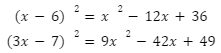
Różnica kwadratów
W przypadku różnicy kwadratów dwóch liczb warto skorzystać z następującego wzoru skróconego mnożenia:
![]()
Przykłady
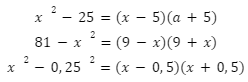
Różnica sześcianów
By obliczyć różnicę sześcianów dwóch liczb, skorzystaj ze wzoru:
![]()
Jak w praktyce wygląda jego wykorzystanie?
Przykład
![]()
Sześcian sumy
Przy obliczaniu sześcianu sumy także warto posiłkować się wzorem, co znacząco przyspieszy wszystkie obliczenia. Wzór ten wygląda następująco:
![]()
Przykład
![]()
Sześcian różnicy
Kolejny równie przydatny wzór skróconego mnożenia dotyczy obliczania sześcianu różnicy. Aby skrócić obliczenia, skorzystaj z poniższego wzoru:
![]()
Przykład:
![]()
Suma sześcianów
Ostatni, jednak tak samo ważny i pomocny wzór skróconego mnożenia odnosi się do obliczania sumy sześcianów. Wzór ten wygląda następująco:
![]()
Przykład
![]()
