Wzorami Viete’a nazywamy wzory wiążące pierwiastki wielomianu z jego współczynnikami. Sama nazwa wzorów pochodzi od nazwiska matematyka – Francois Viete’a. Zanim jednak przejdziemy do wzorów Viete’a dla równania kwadratowego, powróćmy do najważniejszych zagadnień z zakresu równań kwadratowych. Dzięki temu zrozumienie użycia wzorów Viete’a będzie dużo prostsze.
Równanie kwadratowe
Równanie kwadratowe zapisujemy pod postacią wzoru:
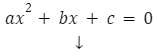a
0
a,b,c 
R – współczynniki równania kwadratowego
x R – zmienna
Wyróżnik równania kwadratowego
Wyróżnik równania kwadratowego to właśnie delta, której wzór warto zapamiętać na długo. Przydaje się on w wielu zadaniach i to nie tylko związanych z funkcją kwadratową.
Przykładowe równania kwadratowe:
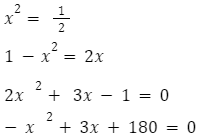
Rozwiązanie równania kwadratowego
Liczba miejsc zerowych funkcji uzależniona jest od wartości delty.
Jeśli:
to równanie kwadratowe będzie mieć dwa rozwiązania. Aby je obliczyć, musisz skorzystać z poniższych wzorów:
to równanie kwadratowe będzie mieć dwa rozwiązania. Aby je obliczyć, musisz skorzystać z poniższych wzorów:
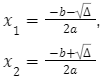
to równanie kwadratowe będzie mieć tylko jedno rozwiązanie. Aby je obliczyć, skorzystaj z wzoru:
Kiedy
, pierwiastek nazywamy pierwiastkiem podwójnym.
to równanie kwadratowe będzie mieć tylko jedno rozwiązanie. Aby je obliczyć, skorzystaj z wzoru:
to równanie kwadratowe nie będzie mieć żadnych rozwiązań.
to równanie kwadratowe nie będzie mieć żadnych rozwiązań.Równanie kwadratowe – wzory Viete’a
Dla równania kwadratowego:
, gdzie a0
mamy dwa rozwiązania 
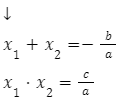
Dzięki powyższym wzorom możemy obliczyć sumę kwadratów pierwiastków w równaniu. Poniższy przykład przedstawia schemat obliczenia z wykorzystaniem wzorów Viete’a.
Przykład
Dane jest równanie:
W pierwszej kolejności sprawdź, czy równanie ma dwa rozwiązania.
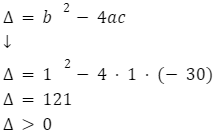
Z powyższego wynika, że wyróżnik jest nieujemny, co oznacza, że równanie ma pierwiastki.
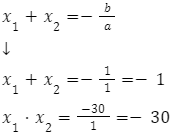
Aby obliczyć sumę kwadratów pierwiastków, korzystamy z wzoru skróconego mnożenia:
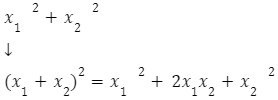
Po przekształceniu powyższe równanie wygląda następująco:
Ostatnim krokiem jest obliczenie sumy kwadratów pierwiastków. Podstawiamy do powyższego wzoru:
Suma kwadratów pierwiastków powyższego równania wynosi 61.
Wzory Viete’a – zastosowanie
Wzory Viete’a sprawdzają się wszędzie tam, gdzie układamy równania kwadratowe lub gdy posiadamy wiedzę o pierwiastkach równania. Bardzo często sięgamy po nie, gdy chcemy sprawdzić, czy pierwiastki równania są określonych znaków. Po powyższym przykładzie możemy także powiedzieć, że dzięki nim możliwe jest znalezienie sumy i iloczynu miejsc zerowych funkcji.
